4 Häufig verwendete Dispersionsmaße
Es gibt vier häufig verwendete Kennzahlen, um die Variabilität (oder Streuung) innerhalb einer Reihe von Kennzahlen anzuzeigen. Dies sind: 1. Bereich 2. Quartilabweichung 3. Durchschnittliche Abweichung 4. Standardabweichung.
Maßnahme Nr. 1. Reichweite:
Der Bereich ist das Intervall zwischen der höchsten und der niedrigsten Punktzahl. Die Reichweite ist ein Maß für die Variabilität oder Streuung der Variationen oder Beobachtungen untereinander und gibt keine Vorstellung von der Streuung der Beobachtungen um einen zentralen Wert.
Symbolisch R = Hs - Ls. Wobei R = Range ist;
Hs ist die höchste Punktzahl und Ls ist die niedrigste Punktzahl.
Berechnung der Reichweite (nicht gruppierte Daten):
Beispiel 1:
Die Ergebnisse von zehn Jungen in einem Test sind:
17, 23, 30, 36, 45, 51, 58, 66, 72, 77.
Beispiel 2
Die Ergebnisse von zehn Mädchen in einem Test sind:
48, 49, 51, 52, 55, 57, 50, 59, 61, 62.
In Beispiel I ist die höchste Punktzahl 77 und die niedrigste Punktzahl ist 17.
Der Bereich ist also der Unterschied zwischen diesen beiden Werten:
. . . Bereich = 77-17 = 60
In ähnlicher Weise in Beispiel II
Bereich = 62 - 48 = 14
Hier stellen wir fest, dass die Anzahl der Jungen weit verstreut ist. Die Anzahl der Jungen variiert daher sehr stark. Die Anzahl der Mädchen variiert jedoch nicht viel (natürlich weniger). Somit ist die Variabilität der Punktzahlen von Jungen mehr als die Variabilität der Punktzahlen von Mädchen.
Berechnung der Reichweite (gruppierte Daten):
Beispiel 3:
Finden Sie den Datenbereich in der folgenden Verteilung:

Lösung:
In diesem Fall ist die obere wahre Grenze der höchsten Klasse 70-79 Hs = 79, 5 und die untere wahre Grenze der niedrigsten Klasse 20-29 ist Ls = 19, 5
Daher ist der Bereich R = Hs - Ls
= 79, 5 - 19, 5 = 60, 00
Der Bereich ist ein Index der Variabilität. Wenn der Bereich größer ist, ist die Gruppe variabler. Je kleiner der Bereich, desto homogener ist die Gruppe. Der Bereich ist das allgemeinste Maß für die "Streuung" oder "Streuung" von Bewertungen (oder Kennzahlen). Wenn wir einen groben Vergleich der Variabilität von zwei oder mehr Gruppen anstellen möchten, können wir den Bereich berechnen.
Der oben angegebene Bereich liegt in einer rohen Form vor oder ist ein absolutes Maß für die Dispersion und ist für Vergleichszwecke ungeeignet, insbesondere wenn die Serien in zwei verschiedenen Einheiten vorliegen. Zu Vergleichszwecken wird der Entfernungskoeffizient durch Division des Bereichs durch die Summe der größten und kleinsten Elemente berechnet.
Vorteile:
1. Die Reichweite kann leicht berechnet werden.
2. Es ist das einfachste Maß für die Dispersion.
3. Es wird berechnet, wenn wir zwei oder mehr Variabilitätsgraphen grob vergleichen wollen.
Einschränkungen:
1. Die Reichweite basiert nicht auf allen Beobachtungen der Serie. Es berücksichtigt nur die extremsten Fälle.
2. Es hilft uns, nur einen groben Vergleich zweier oder mehrerer Variabilitätsgruppen anzustellen.
3. Der Bereich berücksichtigt die beiden Extremwerte einer Serie.
Wenn also N klein ist oder große Lücken in der Häufigkeitsverteilung bestehen, ist der Bereich als Maß für die Variabilität ziemlich unzuverlässig.
Beispiel 4:
Scores der Gruppe A - 3, 5, 8, 11, 20, 22, 27, 33
Hier Bereich = 33 - 3 = 30
Scores der Gruppe B - 3, 5, 8, 11, 20, 22, 27, 93
Hier Bereich = 93 - 3 = 90.
Vergleichen Sie einfach die Ergebnisreihe in Gruppe A und Gruppe B. Wenn in der Gruppe A ein einzelner Score 33 (der letzte Score) auf 93 geändert wird, ändert sich der Bereich stark. Daher kann eine einzige hohe Punktzahl die Reichweite von niedrig nach hoch erhöhen. Deshalb ist die Reichweite kein zuverlässiges Maß für die Variabilität.
4. Es ist sehr stark von Schwankungen in der Probenahme betroffen. Sein Wert ist niemals stabil. In einer Klasse, in der die Schülerhöhe normalerweise zwischen 150 cm und 180 cm liegt, würde der Bereich, wenn ein Zwerg mit einer Höhe von 90 cm zugelassen wird, von 90 cm bis 180 cm hochschießen.
5. Range präsentiert die Serie und die Dispersion nicht wirklich. Asymmetrische und symmetrische Verteilung können den gleichen Bereich haben, jedoch nicht die gleiche Dispersion. Es ist von begrenzter Genauigkeit und sollte mit Vorsicht verwendet werden.
Wir sollten jedoch nicht übersehen, dass der Bereich ein grobes Maß für die Dispersion ist und für genaue und genaue Studien völlig ungeeignet ist.
Maßnahme Nr. 2. Quartilabweichung:
Der Bereich ist das Intervall oder der Abstand auf der Maßskala, der 100-prozentige Fälle einschließt. Die Begrenzungen des Bereichs beruhen nur auf seiner Abhängigkeit von den beiden Extremwerten.
Es gibt einige Dispersionsmaße, die unabhängig von diesen beiden Extremwerten sind. Am häufigsten ist die Quartilabweichung, die auf dem Intervall basiert, das die mittleren 50 Prozent der Fälle in einer bestimmten Verteilung enthält.
Die Quartilabweichung ist die Hälfte der Skalenentfernung zwischen dem dritten und dem ersten Quartil. Es ist der Halbinterquartilbereich einer Verteilung:
Bevor wir die Abweichung des Quartils aufnehmen, müssen wir die Bedeutung von Quartalen und Quartilen kennen.

Ein Test führt beispielsweise zu 20 Punkten und diese Werte sind in absteigender Reihenfolge angeordnet. Wir teilen die Verteilung der Wertungen in vier gleiche Teile auf. Jeder Teil wird ein "Viertel" darstellen. In jedem Quartal gibt es 25% (oder 1/4 von N) Fällen.
Da die Ergebnisse in absteigender Reihenfolge angeordnet sind,
Die ersten 5 Punkte werden im 1. Quartal sein,
Die nächsten 5 Punkte werden im 2. Quartal sein,
Die nächsten 5 Punkte werden im 3. Quartal sein und
Und die niedrigsten 5 Punkte werden im 4. Quartal sein.
Um die Zusammensetzung einer Serie besser studieren zu können, kann es erforderlich sein, sie in drei, vier, sechs, sieben, acht, neun, zehn oder hundert Teile zu unterteilen.
Normalerweise ist eine Serie in vier, zehn oder hundert Teile unterteilt. Ein Artikel unterteilt die Serie in zwei Teile, drei Artikel in vier Teile (Quartile), neun Artikel in zehn Teilen (Dezile) und neunundneunzig Artikel in hundert Teilen (Perzentile).
Es gibt also drei Viertel, neun Dezile und neunundneunzig Perzentile in einer Reihe. Das zweite Quartil oder das 5. Dezil oder das 50. Perzentil ist der Median (siehe Abbildung).
Der Wert des Elements, das die erste Hälfte einer Serie (mit Werten unter dem Medianwert) in zwei gleiche Teile teilt, wird als erstes Quartil (Q 1 ) oder als unteres Quartil bezeichnet. Mit anderen Worten, Q 1 ist ein Punkt, unter dem 25% der Fälle liegen. Q 1 ist das 25. Perzentil.
Das zweite Quartil (Mdn) oder das mittlere Quartil ist der Median. Mit anderen Worten, es ist ein Punkt, unter dem 50% der Punkte liegen. Ein Median ist das 50. Perzentil.
Der Wert des Elements, das die zweite Hälfte der Serie (mit Werten, die über dem Medianwert liegen) in zwei gleiche Teile teilt, wird als drittes Quartil (Q 3 ) oder oberes Quartil bezeichnet. Mit anderen Worten, Q 3 ist ein Punkt, unter dem 75% der Punkte liegen. Q 3 ist das 75. Perzentil.
Hinweis:
Ein Student muss klar zwischen einem Viertel und einem Quartil unterscheiden. Viertel ist ein Bereich; aber Quartil ist ein Punkt auf der Skala. Quartale sind von oben nach unten (oder von der höchsten zur niedrigsten Punktzahl) nummeriert, aber die Quartile sind von unten nach oben nummeriert.
Die Quartilabweichung (Q) ist die Hälfte der Skalenentfernung zwischen dem dritten Quartil (Q 3 ) und dem ersten Quartil (Q 1 ):

L = Untergrenze des ci, in dem Q 3 liegt
3N / 4 = 3/4 von noch 75% von N.
F = Summe aller Frequenzen unter 'L'
fq = Frequenz des ci, auf dem Q 3 liegt und i = Größe oder Länge des ci

L = Untergrenze des ci, in dem Q 1 liegt
N / 4 = ein Viertel (oder 25%) von N,
F = Summe aller Frequenzen unter 'L'
fq = Frequenz des ci, auf dem Q 1 liegt
und i = Größe oder Länge von ci
Inter-Quartil-Bereich:
Der Bereich zwischen dem dritten Quartil und dem ersten Quartil wird als Inter-Quartil-Bereich bezeichnet. Symbolischer Intervallbereich = Q 3 - Q 1 .
Halbinterquartiler Bereich:
Es ist die Hälfte des Abstands zwischen dem dritten und dem ersten Quartil.
Somit ist SI R = Q 3 - Q 1/4
Q- oder Quartilabweichung ist ansonsten als semi-interquartile range (oder SIR) bekannt.
Somit ist Q = Q 3 - Q 1/2
Wenn wir die Formel von Q 3 und Q 1 mit der Medianformel vergleichen, werden die folgenden Beobachtungen klar sein:
ich. Im Median verwenden wir N / 2, während wir für Q 1 N / 4 und für Q 3 3N / 4 verwenden.
ii. Im Medianfall bezeichnen wir mit fm die Häufigkeit von ci, auf der der Median liegt. im Fall von Q 1 und Q 3 bezeichnen wir mit fq die Frequenz des ci, auf dem Q 1 oder Q 3 liegt.
Berechnung von Q (nicht gruppierte Daten):
Um Q zu berechnen, müssen wir zuerst Q 3 und Q 1 berechnen. Q 1 und Q 3 werden auf dieselbe Weise berechnet, wie wir den Median berechnet haben.
Die einzigen Unterschiede sind:
(i) im Medianfall zählten wir 50% (N / 2) von unten, aber
(ii) Im Falle von Q 1 müssen wir 25% der Fälle (oder N / 4) von unten zählen
(iii) Im Falle von Q 3 müssen wir 75% der Fälle (oder 3N / 4) von unten zählen.
Beispiel 5
Ermitteln Sie Q aus den folgenden Bewertungen 20, 21, 22, 23, 24, 25, 26, 27, 28, 29, 30, 31, 32, 33, 34, 35, 36, 37, 38, 39.
Es gibt 20 Punkte.
25% von N = 20/4 = 5
Q 1 ist ein Punkt, unter dem 25% der Fälle liegen. In diesem Beispiel ist Q 1 ein Punkt, unter dem 5 Fälle liegen. Aus der reinen Prüfung der bestellten Daten ergibt sich, dass es unter 24, 5 5 Fälle gibt. Somit ist Q 1 = 24, 5
Ebenso ist Q 3 ein Punkt, unter dem 75% der Abgaben liegen.
75% von N = 3/4 × 20 = 15
Wir finden, dass unter 34, 5, 15 Fälle liegen
Somit ist Q 3 = 34, 5.

In einer symmetrischen Verteilung liegt der Medianwert in der Mitte der Skala von Q 1 und Q 3 . Daher gibt der Wert Q 1 + Q oder Q 3 - Q den Medianwert an. Im Allgemeinen sind Verteilungen jedoch nicht symmetrisch, sodass Q 1 + Q oder Q 3 - Q nicht den Wert des Medianwerts ergeben.
Berechnung von Q (gruppierte Daten):
Beispiel 6:
Die Ergebnisse, die von 36 Studenten in einem Test erhalten wurden, sind in der Tabelle aufgeführt. Finden Sie die Abweichung des Quartils der Ergebnisse.

In Spalte 1 haben wir die Klasse Interval genommen, in Spalte 2 haben wir die Häufigkeit genommen, und in Spalte 3 wurden die kumulativen Häufigkeiten beginnend von unten geschrieben.
Hier ist N = 36, also müssen wir für Q 1 N / 4 = 36/4 = 9 Fälle und für Q 3 3N / 4 = 3 x 36/4 = 27 Fälle nehmen. Bei Betrachtung von Spalte 3 wird cf = 9 in ci 55 - 59 eingeschlossen, deren tatsächliche Grenze bei 54, 5 - 59, 5 liegt. Q1 würde im Intervall von 54, 5 bis 59, 5 liegen.
Der Wert von Q 1 ist wie folgt zu berechnen:

Für die Berechnung von Q 3 wird cf = 27 in ci 65 - 69 eingeschlossen, deren tatsächliche Grenzen 64 sind. 5 - 69, 5. Q 3 würde also im Intervall 64.5 - 69.5 liegen und sein Wert ist wie folgt zu berechnen:

Interpretation der Quartilabweichung:
Bei der Interpretation des Wertes der Quartilabweichung ist es besser, die Werte für Median, Q 1 und Q 3 zusammen mit Q zu verwenden. Wenn der Wert von Q größer ist, ist die Streuung größer, aber der Wert hängt wiederum von der Skala ab der Messung. Zwei Werte von Q sind nur zu vergleichen, wenn die verwendete Skala dieselbe ist. Q, gemessen für Punktzahlen von 20, kann nicht direkt mit Q für Punktzahlen von 50 verglichen werden.
Wenn Median und Q bekannt sind, können wir sagen, dass 50% der Fälle zwischen 'Median - Q' und 'Median + Q' liegen. Dies sind die mittleren 50% der Fälle. Hier erfahren wir nur die mittleren 50% der Fälle. Wie die unteren 25% der Fälle und die oberen 25% der Fälle verteilt sind, ist durch diese Maßnahme nicht bekannt.
Manchmal sind die Extremfälle oder -werte nicht bekannt. In diesem Fall besteht die einzige Alternative für uns darin, die Median- und Quartilabweichung als Maß für die Mitte, die Tendenz und die Streuung zu berechnen. Durch Median und Quartile können wir auf die Symmetrie oder Schiefe der Verteilung schließen. Lassen Sie uns daher eine Vorstellung von symmetrischen und schiefen Verteilungen machen.
Symmetrische und verdrehte Verteilungen:
Eine Verteilung wird als symmetrisch bezeichnet, wenn die Frequenzen symmetrisch um das Maß der zentralen Tendenz verteilt sind. Mit anderen Worten, wir können sagen, dass die Verteilung symmetrisch ist, wenn die Werte, die auf beiden Seiten des Maßes der zentralen Tendenz gleich groß sind, gleiche Frequenzen haben.
Beispiel 7:
Finden Sie heraus, ob die angegebene Verteilung symmetrisch ist oder nicht.

Hier ist das Maß der zentralen Tendenz, sowohl der Mittelwert als auch der Medianwert, 5. Wenn wir die Frequenzen der Werte auf den beiden Seiten von 5 vergleichen, stellen wir fest, dass die Werte 4 und 6, 3 und 7, 2 und 8, 1 sind und 9, 0 und 10 haben die gleiche Anzahl von Frequenzen. Die Verteilung ist also vollkommen symmetrisch.
In einer symmetrischen Verteilung sind Mittelwert und Medianwert gleich und der Median liegt in gleichem Abstand von den beiden Quartilen, dh Q 3 - Median = Median - Q 1 .
Wenn eine Verteilung nicht symmetrisch ist, bezieht sich die Abweichung von der Symmetrie auf ihre Schiefe. Die Neigung zeigt an, dass die Kurve mehr zur einen Seite hin gedreht ist als zur anderen. Die Kurve wird also auf einer Seite einen längeren Schwanz haben.
Die Schrägheit wird als positiv bezeichnet, wenn sich der längere Schwanz auf der rechten Seite befindet, und es wird auf den negativen Wert hingewiesen, wenn sich der längere Schwanz auf der linken Seite befindet.
Die folgenden Abbildungen zeigen das Auftreten einer positiv und negativ geneigten Kurve:

Q 3 - Mdn> Mdn - Q 1 zeigt die Neigung von + ve an
Q 3 - Mdn <Mdn - Q 1 zeigt - ve Schiefe an
Q 3 - Mdn = Mdn - Q 1 zeigt die Nullpunktverschiebung an
Verdienste von Q:
1. Es ist ein repräsentativeres und zuverlässigeres Maß für die Variabilität als der Gesamtbereich.
2. Es ist ein guter Index für die Score-Dichte in der Mitte der Verteilung.
3. Quartile sind nützlich, um die Schiefe einer Verteilung anzuzeigen.
4. Wie der Median gilt auch Q für Open-End-Verteilungen.
Wo immer der Median als Maß für die zentrale Tendenz bevorzugt wird, ist die Quartilabweichung als Maß für die Dispersion bevorzugt.
Einschränkungen von Q:
1. Wie der Median ist die Quartilabweichung jedoch nicht für eine algebraische Behandlung geeignet, da nicht alle Werte der Verteilung berücksichtigt werden.
2. Es berechnet nur das dritte und das erste Quartil und spricht uns über den Bereich aus. Von Q 'können wir kein genaues Bild darüber erhalten, wie die Bewertungen vom zentralen Wert abweichen. Das heißt, "Q" gibt uns keine Vorstellung von der Zusammenstellung der Partituren. 'Q' von zwei Serien kann gleich sein, aber Serien können in der Zusammensetzung ziemlich unterschiedlich sein.
3. Es gibt ungefähr eine Vorstellung von der Dispersion.
4. Die Werte über dem dritten Quartil und die Werte unter dem ersten Quartil werden ignoriert. Es spricht uns einfach von den mittleren 50% der Verteilung.
Verwendung von Q:
1. Wenn der Median ein Maß für eine zentrale Tendenz ist;
2. Wenn die Verteilung an einem Ende unvollständig ist;
3. Wenn es zerstreute oder extreme Punkte gibt, die den SD überproportional beeinflussen würden;
4. Wenn die Konzentration um den Medianwert - die mittleren 50% der Fälle - von vorrangigem Interesse ist.
Quartilabweichungskoeffizient:
Die Quartilabweichung ist ein absolutes Maß für die Streuung, und um sie relativ zu machen, berechnen wir den 'Koeffizienten der Quartilabweichung'. Der Koeffizient wird durch Division der Quartilabweichung durch den Durchschnitt der Quartile berechnet.
Es ist gegeben durch:
Quartilabweichungskoeffizient = Q 3 - Q 1 / Q 3 + Q 1
Dabei beziehen sich Q 3 und Q 1 auf obere bzw. untere Quartile.
Maßnahme Nr. 3. Durchschnittliche Abweichung (AD) oder mittlere Abweichung (MD):
Da wir bereits den Bereich besprochen haben, gibt uns das 'Q' eine grobe Vorstellung von Variabilität. Der Bereich von zwei Serien kann derselbe sein oder die Quartilabweichung von zwei Serien kann derselbe sein, jedoch können sich die beiden Serien unterscheiden. Weder der Bereich noch das 'Q' sprechen von der Komposition der Serie. Diese beiden Kennzahlen berücksichtigen nicht die Einzelwerte.
Die Methode der durchschnittlichen Abweichung oder "mittlere Abweichung", wie sie manchmal genannt wird, neigt dazu, einen gravierenden Mangel beider Methoden (Range und "Q") zu beseitigen. Die durchschnittliche Abweichung wird auch als erster Streuungszeitpunkt bezeichnet und basiert auf allen Elementen einer Serie.
Die durchschnittliche Abweichung ist das arithmetische Mittel der Abweichungen einer Serie, die aus einem bestimmten Maß der zentralen Tendenz (Mittelwert, Median oder Modus) berechnet wird, wobei alle Abweichungen als positiv betrachtet werden. Mit anderen Worten, der Durchschnitt der Abweichungen aller Werte vom arithmetischen Mittelwert wird als mittlere Abweichung oder durchschnittliche Abweichung bezeichnet. (Normalerweise wird die Abweichung vom Mittel der Verteilung abgenommen.)

Wobei total die Gesamtsumme von ist;
X ist die Punktzahl; M ist der Mittelwert; N ist die Gesamtzahl der Punkte.
Und 'd' bedeutet die Abweichung einzelner Werte vom Mittelwert.
Berechnung der mittleren Abweichung (nicht gruppierte Daten):
Beispiel 8:
Finde die mittlere Abweichung für den folgenden Variablensatz:
X = 55, 45, 39, 41, 40, 48, 42, 53, 41, 56
Lösung:
Um die mittlere Abweichung zu ermitteln, berechnen wir zunächst den Mittelwert für die angegebenen Beobachtungen.
Die Abweichungen und die absoluten Abweichungen sind in Tabelle 4.2 angegeben:


Beispiel 9:
Finden Sie die mittlere Abweichung für die unten angegebenen Bewertungen:
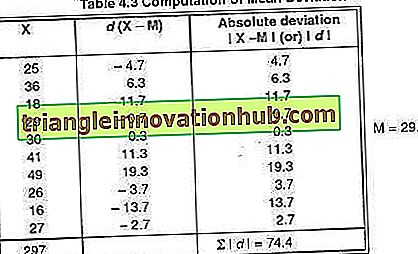
25, 36, 18, 29, 30, 41, 49, 26, 16, 27
Der Mittelwert der obigen Bewertungen betrug 29, 7.
Zur Berechnung der mittleren Abweichung:
Hinweis:
Wenn Sie eine Algebra anwenden, können Sie sehen, dass ∑ (X - M) Null ist

Berechnung der mittleren Abweichung (gruppierte Daten):
Beispiel 10:
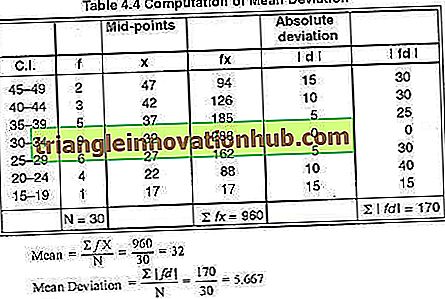
Ermitteln Sie die mittlere Abweichung für die folgende Häufigkeitsverteilung:

Hier in Spalte 1 schreiben wir die CIs, in Spalte 2 schreiben wir die entsprechenden Frequenzen, in Spalte 3 schreiben wir die Mittenpunkte der CIs, die mit 'X' bezeichnet sind, in Spalte 4: Wir schreiben das Produkt aus Frequenzen und Mittelpunkten der mit X bezeichneten ci, in Spalte 5 schreiben wir die absoluten Abweichungen der Mittelpunkt von ci vom Mittelwert, der mit | d | bezeichnet wird In Spalte 6 schreiben wir das Produkt aus absoluten Abweichungen und Häufigkeiten, die mit | fd | bezeichnet werden.
Verdienste der mittleren Abweichung:
1. Die mittlere Abweichung ist das einfachste Maß für die Streuung und berücksichtigt alle Werte in einer bestimmten Verteilung.
2. Es ist leicht verständlich, auch wenn Sie sich mit Statistiken nicht auskennen.
3. Der Wert extremer Gegenstände wird nicht sehr stark beeinflusst.
4. Es ist der Durchschnitt der Abweichungen einzelner Werte vom Mittelwert.
Einschränkungen:
1. Die mittlere Abweichung ignoriert die algebraischen Anzeichen der Abweichungen und kann daher nicht weiter mathematisch behandelt werden. Daher wird es nur als beschreibendes Maß für die Variabilität verwendet.
2. MD wird in der Tat nicht allgemein verwendet. Sie wird in der modernen Statistik nur selten verwendet und im Allgemeinen wird die Streuung anhand der Standardabweichung untersucht.
Verwendung von MD:
1. Wenn es erwünscht ist, alle Abweichungen entsprechend ihrer Größe zu wiegen.
2. Wann es erforderlich ist, zu wissen, in welchem Ausmaß sich die Maßnahmen auf beiden Seiten des Mittelwerts ausbreiten.
3. Wenn extreme Abweichungen die Standardabweichung übermäßig beeinflussen.
Interpretation der mittleren Abweichung:
Für die Interpretation der mittleren Abweichung ist es immer besser, sie zusammen mit dem Mittelwert und der Anzahl der Fälle zu betrachten. Der Mittelwert ist erforderlich, da der Mittelwert und die Mittelwertabweichung jeweils der Punkt und der Abstand auf derselben Messskala sind.
Ohne Mittelwert kann die mittlere Abweichung nicht interpretiert werden, da es keine Anhaltspunkte für die Messskala oder die Maßeinheit gibt. Die Anzahl der Fälle ist wichtig, da das Maß der Streuung davon abhängt. Für eine geringere Anzahl von Fällen ist die Messung wahrscheinlich mehr.
In den beiden Beispielen haben wir:

Im ersten Fall beträgt die mittlere Abweichung fast 25% des Durchschnitts, im zweiten Fall jedoch weniger. Die mittlere Abweichung kann jedoch im ersten Fall aufgrund einer geringeren Anzahl von Fällen größer sein. Die beiden oben berechneten mittleren Abweichungen zeigen also eine nahezu ähnliche Streuung an.
Maßnahme Nr. 4. Standardabweichung oder SD und Abweichung:
Von mehreren Streuungsmaßen ist das am häufigsten verwendete Maß "Standardabweichung". Es ist auch das wichtigste, weil es das einzige Maß für die Dispersion ist, das einer algebraischen Behandlung zugänglich ist.
Dabei werden auch die Abweichungen aller Werte vom Verteilungsmittelwert berücksichtigt. Diese Maßnahme weist die geringsten Nachteile auf und liefert genaue Ergebnisse.
Es beseitigt den Nachteil, dass die algebraischen Zeichen ignoriert werden, während Abweichungen der Elemente vom Durchschnitt berechnet werden. Anstatt die Zeichen zu vernachlässigen, korrigieren wir die Abweichungen und machen sie alle positiv.
Es unterscheidet sich von der AD in mehreren Punkten:
ich. Bei der Berechnung von AD oder MD ignorieren wir Zeichen, während wir bei der Suche nach SD die Schwierigkeit von Zeichen vermeiden, indem wir die einzelnen Abweichungen quadrieren.
ii. Die bei der Berechnung von SD verwendeten quadratischen Abweichungen werden immer vom Mittelwert und nie vom Median oder Modus verwendet.
"Standardabweichung oder SD ist die Quadratwurzel des Durchschnitts der quadratischen Abweichungen der einzelnen Bewertungen vom Mittel der Verteilung."
Um es klarer zu machen, sollten wir hier beachten, dass wir bei der Berechnung des SD alle Abweichungen separat ausgleichen. Finden Sie ihre Summe, dividieren Sie die Summe durch die Gesamtzahl der Punkte und ermitteln Sie dann die Quadratwurzel des Durchschnitts der quadratischen Abweichungen.
SD wird daher auch als 'quadratischer Mittelwertabweichung vom Mittelwert' bezeichnet und wird allgemein mit dem kleinen griechischen Buchstaben σ (Sigma) bezeichnet.
Die Standardabweichung für nicht gruppierte Daten ist symbolisch definiert als:

Wobei d = Abweichung einzelner Werte vom Mittelwert ist;
(Einige Autoren verwenden 'x' als Abweichung einzelner Werte vom Mittelwert.)
∑ = Gesamtsumme von; N = Gesamtzahl der Fälle.
Die mittleren quadratischen Abweichungen werden als Varianz bezeichnet. Oder in einfachen Worten wird das Quadrat der Abweichung als das zweite Streuungsmoment oder Abweichung bezeichnet.
Berechnung von SD (nicht gruppierte Daten):
Es gibt zwei Möglichkeiten, SD für nicht gruppierte Daten zu berechnen:
(a) Direkte Methode
(b) Abkürzungsverfahren.
(a) Direktmethode:
Finden Sie die Standardabweichung für die unten angegebenen Werte:
X = 12, 15, 10, 8, 11, 13, 18, 10, 14, 9
Diese Methode verwendet Formel (18) zum Finden von SD, die die folgenden Schritte beinhaltet:

Schritt 1:
Berechnen Sie das arithmetische Mittel der angegebenen Daten:

Schritt 2:
Schreiben Sie den Wert der Abweichung d, dh X - M, gegen jede Bewertung in Spalte 2. Hier sind die Abweichungen der Bewertungen von 12 zu entnehmen. Nun werden Sie feststellen, dass ∑d oder ∑ (X - M) gleich Null ist. Denken Sie, warum ist es so? Prüfen Sie. Ist dies nicht der Fall, ermitteln Sie den Berechnungsfehler und beheben Sie ihn.
Schritt 3:
Korrigieren Sie die Abweichungen und schreiben Sie den Wert von d 2 in Spalte 3 gegen jede Bewertung. Ermitteln Sie die Summe der Abweichungen im Quadrat. ∑d 2 = 84.
Tabelle 4.5 Berechnung des SD:


Die erforderliche Standardabweichung beträgt 2, 9.
Schritt 4:
Berechnen Sie den Mittelwert der quadratischen Abweichungen und ermitteln Sie dann die positive Quadratwurzel, um den Wert der Standardabweichung zu erhalten, dh σ.
Unter Verwendung der Formel (19) wird die Varianz σ 2 = ∑d 2 / N = 84/10 = 8, 4 sein
(b) Abkürzungsverfahren:
In den meisten Fällen handelt es sich bei dem arithmetischen Mittel der gegebenen Daten um einen Bruchwert, und dann wird der Prozess, Abweichungen zu nehmen und sie zu quadrieren, bei der Berechnung von SD langwierig und zeitraubend
Um die Berechnung in solchen Situationen zu erleichtern, können die Abweichungen von einem angenommenen Mittelwert genommen werden. Die angepasste Abkürzungsformel für die Berechnung von SD lautet dann

woher,
d = Abweichung der Bewertung von einem angenommenen Mittelwert, z. B. AM; dh d = (X - AM).
d 2 = Das Quadrat der Abweichung.
∑d = Die Summe der Abweichungen.
∑d 2 = Die Summe der Abweichungen im Quadrat.
N = Anzahl der Bewertungen oder Variationen.
Das Berechnungsverfahren wird im folgenden Beispiel erläutert:
Beispiel 11:
Suchen Sie nach SD für die in Tabelle 4.5 angegebenen Werte von X = 12, 15, 10, 8, 11, 13, 18, 10, 14, 9. Verwenden Sie die Abkürzungsmethode.
Lösung:
Nehmen wir als Mittelwert AM = 11 an.
Die Abweichungen und Quadrate der in der Formel erforderlichen Abweichungen sind in der folgenden Tabelle angegeben:
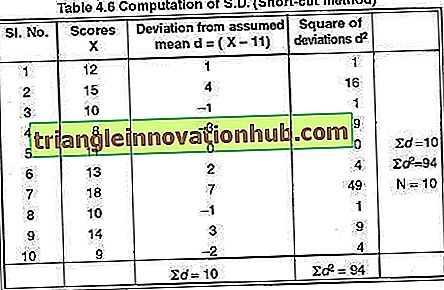
Setzen Sie die Werte aus der Tabelle in die Formel, den SD

Die Abkürzungsmethode ergibt das gleiche Ergebnis, das wir mit der direkten Methode des vorherigen Beispiels erhalten haben. Die Abkürzungsmethode verringert jedoch die Berechnungsarbeit in Situationen, in denen das arithmetische Mittel keine ganze Zahl ist.
Berechnung von SD (Gruppierte Daten):
(a) Langmethode / Direktmethode:
Beispiel 12:
Suchen Sie das SD für die folgende Verteilung:

Auch hier besteht der erste Schritt darin, den Mittelwert M zu finden, für den wir die mit X 'bezeichneten Mittelpunkte der c.i nehmen und das Produkt f X finden müssen.' Der Mittelwert ist gegeben durch ∑ f x '/ N. Der zweite Schritt besteht darin, die Abweichungen der Mittelpunkte der Klassenintervalle X 'von dem mit d bezeichneten Mittelwert, dh X'-M, zu ermitteln.
Der dritte Schritt besteht darin, die Abweichungen zu quadrieren und das Produkt aus den quadratischen Abweichungen und der entsprechenden Frequenz zu ermitteln.

Um das obige Problem zu lösen, werden ci in Spalte 1 geschrieben, Frequenzen in Spalte 2, Mittelpunkte von c., Dh X 'sind in Spalte 3 geschrieben, das Produkt von f X' ist in Spalte 4 angegeben, die Abweichung von X 'aus dem Mittelwert ist in Spalte 5 geschrieben, die quadratische Abweichung d 2 ist in Spalte 6 angegeben, und das Produkt f d 2 ist in Spalte 7 geschrieben.
Wie nachfolgend dargestellt:
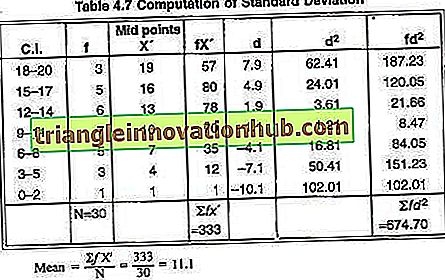
Die Abweichungen der Mittelpunkte sind also aus 11.1 zu entnehmen.

Somit beträgt die erforderliche Standardabweichung 4, 74.
(b) Abkürzungsverfahren:
Bei der direkten Methode wird manchmal beobachtet, dass die Abweichungen vom tatsächlichen Mittelwert in Dezimalzahlen und die Werte von d 2 und fd 2 schwer zu berechnen sind. Um dieses Problem zu vermeiden, verwenden wir eine Short-Cut-Methode zur Berechnung der Standardabweichung.
Bei dieser Methode nehmen wir nicht Abweichungen vom tatsächlichen Mittelwert, sondern Abweichungen von einem geeignet gewählten angenommenen Mittelwert, z. B. AM
Die folgende Formel wird dann zur Berechnung von SD verwendet:

wobei d eine Abweichung vom angenommenen Mittelwert ist.
Die folgenden Schritte werden dann in die Berechnung der Standardabweichung einbezogen:
(i) Abweichungen der Abweichungen vom angenommenen Mittelwert AM erhalten als d = (X - AM)
(ii) Multiplizieren Sie diese Abweichungen mit entsprechenden Frequenzen, um die Spalte fd zu erhalten . Die Summe dieser Spalte ergibt ∑ fd.
fd mit entsprechender Abweichung (d)
(iii) Multiplizieren, um die Spalte fd 2 zu erhalten . Die Summe dieser Spalte ist ∑ fd 2 .
(iv) Verwenden Sie Formel (22), um SD zu finden
Beispiel 13:
Verwenden Sie die Shortcut-Methode find SD der Daten in Tabelle 4.7.
Lösung:
Nehmen wir als Mittelwert AM = 10 an. Weitere Berechnungen zur Berechnung des SD sind in Tabelle 4.8 aufgeführt.

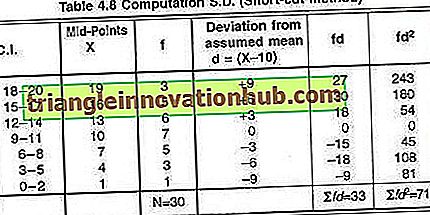
Werte aus der Tabelle übernehmen

Mit der Formel (19) die Varianz

(c) Stufenabweichungsverfahren:
In dieser Methode schreiben wir in Spalte 1 ci's; In Spalte 2 schreiben wir die Frequenzen. In Spalte 3 schreiben wir die Werte von d, wobei d = X'-AM / i ist; In Spalte 4 schreiben wir das Produkt von fd und in Spalte 5 schreiben wir die Werte von fd 2 wie folgt:

Angenommenes Mittel ist der Mittelpunkt von ci 9-11, dh 10, also wurden die Abweichungen d von 10 genommen und durch 3 dividiert, die Länge von ci. Die Formel für SD in der Schrittabweichungsmethode lautet

wo i = Länge der c.i,
f = Frequenz;
d = Abweichungen der Mittelpunkte von ci vom angenommenen Mittelwert (AM) in Einheiten des Klassenintervalls (i), die angegeben werden können:

Werte aus der Tabelle übernehmen

Die Berechnungsverfahren können auch auf folgende Weise angegeben werden:

Kombinierte Standardabweichung ( σ com b ):
Wenn zwei Sätze von Bewertungen zu einem einzigen Los zusammengefasst wurden, ist es möglich, das σ der Gesamtverteilung aus den σ 's der beiden Komponentenverteilungen zu berechnen.
Die Formel lautet:

wobei σ 1 = SD der Verteilung 1
σ 2 = SD der Verteilung 2
d 1 = (M 1 - M Kamm )
d 2 = (M 2 - M Kamm )
N 1 = Anzahl der Fälle in der Verteilung 1.
N 2 = Anzahl der verteilten Fälle 2.
Ein Beispiel veranschaulicht die Verwendung der Formel.
Beispiel 14:
Angenommen, wir erhalten die Mittel und SDs für einen Leistungstest für zwei Klassen unterschiedlicher Größe und werden gebeten, das o der kombinierten Gruppe zu finden.
Daten sind wie folgt:

Zuerst finden wir das

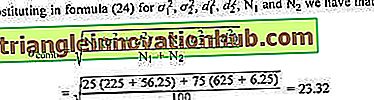
Die Formel (24) kann auf eine beliebige Anzahl von Verteilungen erweitert werden. Bei drei Distributionen ist dies beispielsweise der Fall

Eigenschaften von SD:
1. Wenn jeder Wert der Variablen um den gleichen konstanten Wert erhöht wird, bleibt der Wert von SD der Verteilung unverändert:
Wir werden diesen Effekt auf SD anhand einer Illustration besprechen. Die Tabelle (4.10) zeigt Originalbewertungen von 5 Schülern in einem Test mit einem arithmetischen Mittelwert von 20.
Neue Bewertungen (X ') werden auch in derselben Tabelle angegeben, die wir erhalten, indem jeder ursprünglichen Bewertung eine Konstante 5 hinzugefügt wird. Anhand einer Formel für nicht gruppierte Daten beobachten wir, dass der SD der Scores in beiden Situationen gleich bleibt.


Somit bleibt der Wert von SD in beiden Situationen gleich.
2. Wenn von jeder Variablen ein konstanter Wert abgezogen wird, bleibt der Wert von SD der neuen Verteilung unverändert:
Die Schüler können auch prüfen, dass, wenn wir eine Konstante von jeder Punktzahl subtrahieren, der Mittelwert um die Konstante verringert wird, aber SD gleich ist. Dies liegt daran, dass ' d ' unverändert bleibt.
3. Wenn jeder beobachtete Wert mit einem konstanten Wert multipliziert wird, werden auch SD der neuen Beobachtungen mit derselben Konstante multipliziert:
Wir multiplizieren jede Punktzahl der ursprünglichen Verteilung (Tabelle 4.10) mit 5.

Daher wird der SD der neuen Verteilung mit derselben Konstante multipliziert (hier sind es 5).
4. Wenn jeder beobachtete Wert durch einen konstanten Wert geteilt wird, werden auch SD der neuen Beobachtungen durch dieselbe Konstante geteilt. Die Studierenden können anhand eines Beispiels untersuchen:
Abschließend sei gesagt, SD ist unabhängig von Ursprungsänderung (Addition, Subtraktion), aber von Skalenänderung (Multiplikation, Division).
Messungen der relativen Dispersion (Variationskoeffizient):
Die Streuungsmaße geben uns eine Vorstellung davon, inwieweit die Bewertungen um ihren zentralen Wert verteilt sind. Daher können zwei Häufigkeitsverteilungen mit den gleichen zentralen Werten mit Hilfe verschiedener Streuungsmessungen direkt verglichen werden.
Wenn zum Beispiel bei einem Test in einer Klasse Jungen die mittlere Punktzahl M 1 = 60 mit SD σ 1 = 15 und die mittlere Punktzahl der Mädchen M 2 = 60 mit SD σ 2 = 10 hat. Mädchen mit einem geringeren SD haben eindeutig einen Wert, sind bei der Bewertung ihrer durchschnittlichen Punktzahl gleichbleibender als Jungen.
Es gibt Situationen, in denen zwei oder mehr Verteilungen mit ungleichen Mitteln oder unterschiedlichen Maßeinheiten hinsichtlich ihrer Streuung oder Variabilität zu vergleichen sind. Für solche Vergleiche verwenden wir relative Dispersionskoeffizienten oder Variationskoeffizienten (CV).
Die Formel lautet:

(Variationskoeffizient oder Koeffizient der relativen Variabilität)
V gibt den Prozentsatz an, der von dem Testmittelwert ist. Es ist also ein von den Maßeinheiten unabhängiges Verhältnis.
V ist aufgrund bestimmter Unklarheiten bei der Interpretation in seiner Verwendung eingeschränkt. Bei Verhältnissen ist dies vertretbar - Skalen, bei denen die Einheiten gleich sind und es einen echten Null- oder Bezugspunkt gibt.
Zum Beispiel kann V ohne zu zögern mit physikalischen Skalen verwendet werden - denjenigen, die lineare Größen, Gewicht und Zeit betreffen.
Zwei Fälle treten bei der Verwendung von V mit Ratio-Skalen auf:
(1) Wenn sich die Einheiten nicht unterscheiden, und
(2) Wenn M ungleich sind, sind die Einheiten der Skala gleich.
1. Wenn Einheiten anders sind als:
Beispiel 15
Eine Gruppe von 10-jährigen Jungen hat eine durchschnittliche Höhe von 137 cm. mit einem o von 6, 2 cm. Die gleiche Gruppe von Jungen hat ein Durchschnittsgewicht von 30 kg. mit einem von 3, 5 kg. In welcher Eigenschaft ist die Gruppe variabler?
Lösung:
Natürlich können wir Zentimeter und Kilogramm nicht direkt vergleichen, aber wir können die relative Variabilität der beiden Verteilungen in V vergleichen.
Im vorliegenden Beispiel unterscheiden sich zwei Gruppen nicht nur hinsichtlich des Mittelwerts, sondern auch in Maßeinheiten, nämlich cm. im ersten Fall und kg. in dieser Sekunde. Der Variationskoeffizient kann verwendet werden, um die Variabilität der Gruppen in einer solchen Situation zu vergleichen.
Wir berechnen also:

Aus der obigen Berechnung ergibt sich, dass diese Jungen ungefähr doppelt so schwer wiegen (11, 67 / 4, 53 = 2, 58).
2. Wenn die Mittel ungleich sind, die Skaleneinheiten jedoch gleich sind :
Angenommen, wir haben die folgenden Daten zu einem Test für eine Gruppe von Jungen und eine Gruppe von Männern:

Dann vergleichen Sie:
(i) Die Leistung der beiden Gruppen im Test.
(ii) Die Variabilität der Bewertungen in den beiden Gruppen.
Lösung:
(i) Da die Durchschnittspunktzahl der Jungengruppe höher ist als die der Männer, hat die Jungengruppe den Test besser bewertet.
(ii) Zum Vergleich zweier Gruppen hinsichtlich der Variabilität zwischen den Bewertungen wird der Variationskoeffizient berechnet: V der Jungen = 26, 67 und V der Männer = 38, 46.
Daher ist die Variabilität der Bewertungen in der Männergruppe größer. Die Schülerinnen und Schüler in der Jungengruppe, die einen geringeren Lebenslauf haben, erzielen im Vergleich zu der Männergruppe eine einheitlichere Bewertung ihrer Durchschnittspunktzahl.
SD und die Verbreitung von Beobachtungen:
In einer symmetrischen (normalen) Verteilung
(i) Der Mittelwert ± 1 SD deckt 68, 26% der Ergebnisse ab.
Der Mittelwert ± 2 SD deckt 95, 44% der Ergebnisse ab.
Der Mittelwert ± 3 SD deckt 99, 73% der Ergebnisse ab.
(ii) Bei großen Stichproben (N = 500) beträgt der Bereich etwa das 6fache von SD.
Wenn N ungefähr 100 ist, ist der Bereich ungefähr das Fünffache der SD.
Wenn N ungefähr 50 ist, ist der Bereich ungefähr das 4, 5-fache des SD.
Wenn N ungefähr 20 ist, ist der Bereich ungefähr das 3, 7-fache des SD
Interpretation der Standardabweichung:
Die Standardabweichung kennzeichnet die Art der Verteilung der Ergebnisse. Wenn die Bewertungen weiter verbreitet sind, ist SD größer und wenn die Bewertungen weniger gestreut sind, ist SD geringer. Um den Wert des Streuungsmaßes zu interpretieren, müssen wir verstehen, dass je größer der Wert von ' σ ' ist, desto mehr Streuungen sind die Werte aus dem Mittelwert.
Wie bei der mittleren Abweichung erfordert die Interpretation der Standardabweichung den Wert von M und N zur Berücksichtigung.
In den folgenden Beispielen sind die erforderlichen Werte für σ, Mittelwert und N wie folgt angegeben:

Hier ist die Dispersion in Beispiel 2 mehr als in Beispiel 1. Dies bedeutet, dass die Werte in Beispiel 2 stärker gestreut sind als in Beispiel 1.
Vorzüge von SD:
1. SD ist starr definiert und sein Wert ist immer eindeutig.
2. Es ist das am weitesten verbreitete und wichtigste Maß für die Dispersion. Es nimmt eine zentrale Stellung in der Statistik ein.
3. Wie die mittlere Abweichung basiert sie auf allen Werten der Verteilung.
4. Hier werden die Anzeichen von Abweichungen nicht ignoriert, sondern sie werden durch Quadrieren der Abweichungen eliminiert.
5. Es ist das wichtigste Maß für die Variabilität, da es einer algebraischen Behandlung zugänglich ist und in der Korrelationsarbeit und in der weiteren statistischen Analyse verwendet wird.
6. Es ist weniger von Schwankungen der Probenahme betroffen.
7. Es ist das verlässlichste und genaueste Maß für die Variabilität. SD geht immer mit dem Mittelwert aus, der das verlässlichste Maß für die zentrale Tendenz darstellt.
8. Sie liefert eine Standardmaßeinheit, die von Test zu Test eine vergleichbare Bedeutung besitzt. Darüber hinaus steht die Normalkurve in direktem Zusammenhang mit SD
Einschränkungen:
1. Es ist nicht leicht zu berechnen und es ist nicht leicht zu verstehen.
2. Sie gibt extremen Gegenständen mehr Gewicht und weniger denjenigen, die nahe am Mittelwert liegen. Wenn die Abweichung einer extremen Punktzahl quadriert wird, führt dies zu einem größeren Wert.
Verwendung von SD:
Standardabweichung wird verwendet:
(i) Wenn das genaueste, zuverlässigste und stabilste Maß der Variabilität gewünscht wird.
(ii) Wenn extremen Abweichungen vom Mittelwert mehr Gewicht beigemessen werden soll.
(iii) Wenn anschließend der Korrelationskoeffizient und andere Statistiken berechnet werden.
(iv) Wenn Zuverlässigkeitsmaße berechnet werden.
(v) Wenn Scores richtig in Bezug auf die Normalkurve interpretiert werden sollen.
(vi) Wenn Standardwerte berechnet werden sollen.
(vii) Wenn wir die Signifikanz der Differenz zwischen zwei Statistiken testen wollen.
(viii) Wenn der Variationskoeffizient, die Varianz usw. berechnet werden.