Die wichtigen Methoden zur Messung der Preiselastizität der Versorgung
Einige der wichtigsten Methoden zur Messung der Preiselastizität des Angebots sind wie folgt!
Dieses Konzept entspricht dem Konzept der Preiselastizität der Nachfrage. Sie weist auf die Reaktion der Verkäufer auf eine bestimmte Preisänderung der Ware hin. Es erklärt die quantitativen Änderungen des Angebots einer Ware aufgrund einer bestimmten Preisänderung der Ware.
Die Preiselastizität des Angebots bezieht sich auf den Reaktionsgrad der Lieferung einer Ware in Bezug auf die Änderung des Preises dieser Ware.
Methoden zur Messung der Preiselastizität der Lieferung:
Die Preiselastizität des Angebots kann nach folgenden Methoden gemessen werden:
1. prozentuale Methode
2. Geometrische Methode
Lassen Sie uns diese Methoden im Detail diskutieren.
1. prozentuale Methode:
Wie bei der Nachfrageelastizität ist die am häufigsten verwendete Methode zur Messung der Preiselastizität des Angebots (E s ) die prozentuale Methode. Diese Methode wird auch als "proportionale Methode" bezeichnet.
Nach diesem Verfahren wird die Elastizität als Verhältnis der prozentualen Änderung der Liefermenge zu der prozentualen Änderung des Preises gemessen.
Preiselastizität des Angebots (E s ) = prozentuale Änderung der gelieferten Menge / prozentuale Änderung des Preises
Woher:
1. prozentuale Änderung der Liefermenge = Änderung der Liefermenge (∆Q) / Ausgangsmenge (Q) x 100
2. Änderung der Menge (∆Q) = Neue Menge (Q 1 ) - Anfangsmenge (Q)
3. Prozentuale Änderung des Preises = Änderung des Preises (∆P) / Anfangsmenge (P) × 100
4. Änderung des Preises (∆P) = Neuer Preis (P 1 ) - Anfangspreis (P)
Anteilige Methode:
Die prozentuale Methode kann auch in die proportionale Methode umgerechnet werden. Setzt man die Werte 1, 2, 3 und 4 in die Methode der Prozentmethode, erhält man:
Es ist = Q / Q · 100 / · P / P · 100
Es ist = Q / Q / P / P
Versorgungselastizität (anteilige Methode) = ∆Q / ∆P x P / Q
Woher:
Q = gelieferte Anfangsmenge
∆Q = Änderung der Liefermenge
P = Anfangspreis
∆P = Preisänderung
Um die prozentuale / proportionale Methode zu veranschaulichen, betrachten wir ein Beispiel:
Beispiel: Angenommen, zum Preis von Rs. 10 pro Einheit liefert ein Unternehmen 50 Einheiten einer Ware. Wenn der Preis auf Rs steigt. 12 pro Einheit erhöht die Firma den Vorrat auf 70 Einheiten.
Die Preiselastizität der Lieferung wird wie folgt berechnet:
Preiselastizität des Angebots (E S ) = prozentuale Änderung der gelieferten Menge / prozentuale Änderung des Preises
Jetzt,
Prozentuale Änderung der Liefermenge = Änderung der Liefermenge (∆Q) / Ausgangsmenge (Q) × 100
= (70-50) / 50 × 100 = 40%
Prozentuale Änderung des Preises = Änderung des Preises (∆P) / Anfangspreis (P) × 100
= (12-10) / 10 × 100 = 20%
E S = 40% / 20% = 2
Die Preiselastizität der Lieferung ist positiv:
Bisher haben wir gesehen, dass das Konzept der Angebotselastizität dem Konzept der Nachfrageelastizität ähnelt. Es gibt jedoch einen Unterschied. Die Angebotselastizität hat immer ein positives Vorzeichen gegenüber dem negativen Anzeichen der Nachgiebigkeit der Nachfrage. Dies geschieht aufgrund des direkten Zusammenhangs zwischen Preis und Liefermenge.
2. Geometrische Methode:
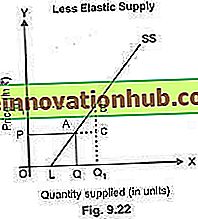
Gemäß der geometrischen Methode wird die Elastizität an einem bestimmten Punkt der Versorgungskurve gemessen. Diese Methode wird auch als "Arc-Methode" oder "Punktmethode" bezeichnet. Die Messung der Versorgungselastizität für die Versorgungskurve SS (z. B. an Punkt A) ist in Abb. 9.20 dargestellt:

Bei Punkt "A" in der Abbildung ist der Preis OP und die gelieferte Menge OQ. Wenn der Preis auf OP 1 steigt, steigt auch die gelieferte Menge auf OQ 1 . Die Angebotskurve wird über die Y-Achse hinaus verlängert, so dass sie am Punkt 'L' auf die verlängerte X-Achse trifft. Nun ist an Punkt A die Elastizität des Angebots gleich:
E S = ∆Q / ∆P × P / Q
Symbole haben die übliche Bedeutung, wie unter "Prozentmethode" beschrieben.
Aus dem Diagramm ergibt sich ∆Q = QQ 1 ; ∆P = OP und Q = OQ
Wenn wir diese Werte in die Formel setzen, erhalten wir:
E S = QQ 1 / PP 1 × OP / OQ
QQ 1 = AC; PP 1 = BC und OP = AQ. Wenn wir diese Werte in (1) einsetzen, erhalten wir
ES = AC / BC × AQ / OQ
Nun sind ∆BAC und ∆ALQ aufgrund von AAA-Eigenschaft ähnliche Dreiecke. Das bedeutet, dass das Verhältnis ihrer Seiten gleich ist.
Dies impliziert:
AC / BC = LQ / AQ
Wenn Sie den Wert von (3) in (2) einsetzen, erhalten wir:
E S = LQ / AQ × AQ / OQ
Oder einfach: E S = LQ / OQ = Intercept auf der X-Achse / Zu diesem Preis gelieferte Menge
Lassen Sie uns nun die drei verschiedenen Fälle der geometrischen Methode diskutieren: (i) Hochelastische Versorgung; (ii) einheitliche elastische Versorgung; und (iii) weniger elastische Versorgung.
(i) Hochelastische Versorgung (E s > 1):
Eine Versorgungskurve, die durch die Y-Achse verläuft und an einem bestimmten Punkt (z. B. L in Abb. 9.20) auf die verlängerte X-Achse trifft, ist hoch elastisch. In Abb. 9.20 ist die Versorgungselastizität (E s ) = und LQ / OQ und LQ> OQ
Da LQ größer als OQ ist, ist die Versorgungselastizität am Punkt A größer als eins (hochelastisch). Im Allgemeinen können wir sagen, dass eine Versorgungskurve für eine gerade Linie, die durch die Y-Achse verläuft oder einen negativen Schnittpunkt auf der X-Achse aufweist, hochelastisch ist (E s > 1).
(ii) Einheitliche elastische Versorgung (E s = 1):
Wenn die geradlinige Versorgungskurve den Ursprung durchläuft (siehe Versorgungskurve SS in Abb. 9.21), ist die Versorgungselastizität gleich eins. Im Diagramm ist
Versorgungselastizität (Es) = OQ / OQ = 1. Daher ist die Versorgung ist einheitlich elastisch.

(iii) weniger elastische Versorgung (E s <1):
Wenn ferner eine Versorgungskurve an einem bestimmten Punkt auf die X-Achse trifft, beispielsweise L in Abb. 9.22, dann ist die Versorgung unelastisch. Wie aus dem Diagramm ersichtlich, ist E = LQ / OQ und LQ> OQ. Also ist E <1, dh der Vorrat ist weniger elastisch.