Bedeutung des Unterschieds zwischen den Mitteln

Nachdem Sie diesen Artikel gelesen haben, lernen Sie die Bedeutung des Unterschieds zwischen den Mitteln kennen.

Angenommen, wir möchten testen, ob sich 12-jährige Jungen und 12-jährige Mädchen an öffentlichen Schulen in ihren mechanischen Fähigkeiten unterscheiden. Da die Populationen dieser Jungen und Mädchen zu groß sind, nehmen wir eine Stichprobe dieser Jungen und Mädchen, führen einen Test durch und berechnen die Mittel von Jungen und Mädchen getrennt.

Angenommen, die durchschnittliche Punktzahl solcher Jungen liegt bei 50 und die der Mädchen bei 45. Wir unterscheiden zwischen den Mitteln von Jungen und Mädchen einen Unterschied von 5 Punkten. Es kann sein, dass eine solche Differenz aufgrund von Schwankungen der Abtastung entstanden sein könnte.

Wenn wir zwei weitere Proben ziehen, eine aus der Bevölkerung von 12-jährigen Jungen und andere aus der Bevölkerung von 12-jährigen Mädchen, werden wir einen Unterschied zwischen den Mitteln feststellen, wenn wir sie bei der Auswahl von Proben für eine lange Zeitspanne wiederholen Bei 12-jährigen Jungen und 12-jährigen Mädchen werden wir feststellen, dass der Unterschied zwischen zwei Arten von Mitteln variieren wird.

Manchmal ist dieser Unterschied positiv, manchmal negativ und manchmal Null. Die Verteilung dieser Differenzen bildet eine Normalverteilung um eine Differenz von Null. Der SD dieser Verteilung wird als Standardfehler der Mittelwertdifferenz bezeichnet.

Dafür werden folgende Symbole verwendet:

SEM ₁ - M ₂ oder SE _D oder σ _DM

Zwei Situationen ergeben sich hinsichtlich der Unterschiede zwischen den Mittelwerten:

a) Mittel, bei denen die Mittel unkorreliert / unabhängig sind, und

(b) diejenigen, bei denen die Mittel korreliert sind.

(a) SE der Differenz zwischen zwei unabhängigen Mitteln:

Die Mittel sind unkorreliert oder unabhängig, wenn sie aus verschiedenen Proben oder aus nicht korrelierten Tests berechnet werden, die derselben Probe verabreicht werden.

In diesem Fall können zwei Situationen auftreten:

(i) Wenn Mittel unkorreliert oder unabhängig sind und die Stichproben groß sind

(ii) Wenn Mittel unkorreliert oder unabhängig sind und die Stichproben klein sind.

(i) SE der Differenz (SE _D ), wenn Mittel unkorreliert oder unabhängig sind und Proben groß sind:

In dieser Situation kann der SE _D nach folgender Formel berechnet werden:

wobei SE _D = Standardfehler der Mittelwertdifferenz

SEm ₁ = Standardfehler des Mittelwerts der ersten Probe

SEm ₂ = Standardfehler des Mittelwerts der zweiten Probe

Beispiel 1:

Zwei Gruppen, eine aus 114 Männern und eine aus 175 Frauen. Die Durchschnittswerte von Männern und Frauen in einem Wortbildungstest waren 19, 7 bzw. 21, 0 und die SD dieser beiden Gruppen waren 6, 08 bzw. 4, 89. Prüfen Sie, ob der beobachtete Unterschied von 1, 3 zu Gunsten von Frauen bei 0, 05 und bei 0, 01 deutlich ist.

Lösung:

Es ist ein zweiseitiger Test → Die Richtung ist nicht klar.

Um die Signifikanz einer erhaltenen Differenz zwischen zwei Stichprobenmitteln zu testen, können wir die folgenden Schritte ausführen:

Schritt 1:

Im ersten Schritt müssen wir uns darüber im Klaren sein, ob wir einen zweiseitigen oder einen einseitigen Test machen wollen. Hier wollen wir testen, ob der Unterschied signifikant ist. Es ist also ein zweiseitiger Test.

Schritt 2:

Wir stellen eine Nullhypothese (H ₀ ) auf, dass es keinen Unterschied zwischen den Bevölkerungsmitteln von Männern und Frauen bei der Wortbildung gibt. Wir nehmen an, dass der Unterschied zwischen den Bevölkerungsmitteln von zwei Gruppen gleich Null ist, dh H _o : D = 0.

Schritt 3:

Dann müssen wir das Signifikanzniveau des Tests bestimmen. In unserem Beispiel testen wir den Unterschied auf der Signifikanzstufe 0, 05 und 0, 01.

Schritt 4:

In diesem Schritt müssen wir den Standardfehler der Differenz zwischen den Mitteln berechnen, dh SE _D.

Da unser Beispiel unkorrelierte Mittelwerte und große Stichproben sind, müssen wir zur Berechnung von SE _D die folgende Formel anwenden:

Schritt 5:

Nach der Berechnung des Wertes von SE _{D müssen} wir die Differenz der Stichprobenmittelwerte in SE _D ausdrücken. Da unser Beispiel ein einfaches Beispiel für große Stichproben ist, müssen wir Z berechnen, wobei

Schritt 6:

In Bezug auf die Art des Tests in unserem Beispiel sollen wir den kritischen Wert für Z aus Tabelle A sowohl auf 0, 05 als auch auf 0, 01-Signifikanzniveau ermitteln.

Aus Tabelle A sind Z.05 = 1.96 und Z.01 = 2.58. (Dies bedeutet, dass der Wert von Z, der bei 0, 05 oder darunter signifikant ist, mindestens 1, 96 betragen muss).

Jetzt 1.91 <1.96, ist der markante Unterschied auf dem Niveau von 0, 05 nicht signifikant (dh H ₀ wird akzeptiert).

Deutung:

Da die Stichprobe groß ist, können wir eine Normalverteilung von Z annehmen. Das erhaltene Z erreicht nicht das 0, 05-Signifikanzniveau, das für große Stichproben 1, 96 beträgt.

Folglich würden wir die Nullhypothese nicht ablehnen und würden sagen, dass der erhaltene Unterschied nicht signifikant ist. Es kann tatsächlich Unterschiede geben, aber wir haben keine ausreichende Gewissheit darüber.

Eine praktischere Schlussfolgerung wäre, dass wir keine ausreichenden Beweise für Geschlechtsunterschiede in der Wortbildungsfähigkeit haben, zumindest in der Art der untersuchten Bevölkerung.

Beispiel 2

Daten zur Leistung von Jungen und Mädchen werden wie folgt angegeben:

Testen Sie, ob die Jungen oder Mädchen bessere Leistungen erbringen und ob der Unterschied von 1, 0 zugunsten der Jungen auf dem Niveau von 0, 05 signifikant ist. Wenn wir den Unterschied als signifikant akzeptieren, was wäre der Fehler Typ 1?

Lösung:

1, 85 <1, 96 (Z 0, 05 = 1, 96). Daher wird H ₀ akzeptiert und der deutliche Unterschied von 1, 0 zugunsten der Jungen ist auf dem Niveau von 0, 05 nicht signifikant.

Wenn wir den Unterschied als signifikant akzeptieren, legen wir einen Fehler vom Typ 1 fest. Beim Lesen von Tabelle A stellen wir fest, dass ± 1.85 Z 93, 56% der Fälle umfasst. Wenn man den markanten Unterschied als signifikant anerkennt, sind wir damit 6, 44% (100 - 93, 56) falsch, so dass der Typ-1-Fehler 0644 ist.

Beispiel 3:

Klasse A wurde in einer intensiven Coaching-Einrichtung unterrichtet, während Klasse B im normalen Unterricht unterrichtet wurde. Am Ende eines Schuljahres waren die Klassen A und B im Durchschnitt 48 und 43 mit SD 6 bzw. 7, 40.

Testen Sie, ob durch intensives Coaching ein Mittelzuwachs der Klasse A erzielt wurde. Die Klasse A besteht aus 60 und B 80 Studenten.

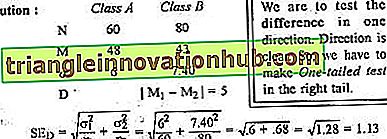
. ^. . 4.42 ist mehr als Z.01 oder 2.33. Also wird H _o abgelehnt. Der deutliche Unterschied ist auf .01 signifikant.

Daraus schließen wir, dass intensives Coaching gute Mittelwerte der Klasse A erzielt hat.

(ii) Die SE der Differenz (SE _D ), wenn Mittel unkorreliert oder unabhängig sind und die Stichproben klein sind:

Wenn die N von zwei unabhängigen Proben klein sind, kann der SE der Differenz zweier Mittelwerte unter Verwendung der folgenden zwei Formeln berechnet werden:

Wenn Punkte vergeben werden:

wobei x ₁ = X ₁ - M _{1 ist} (dh Abweichung der Bewertungen der ersten Probe vom Mittelwert der ersten Probe).

X ₂ = X ₂ - M ₂ (dh Abweichung der Bewertungen der zweiten Probe von ihrem Mittelwert)

Wenn Mittel und SD beider Proben angegeben werden:

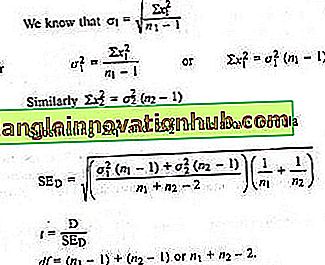
Beispiel 4:

Ein Interessentest wird an 6 Jungen in einer Berufsausbildungsklasse und an 10 Jungen in einer Lateinklasse durchgeführt. Ist der mittlere Unterschied zwischen den beiden Gruppen auf der 0, 05-Ebene signifikant?

D finden wir, dass mit df = 14 der kritische Wert von t auf dem 0, 05-Niveau 2, 14 und auf dem 0, 01-Niveau 2, 98 beträgt. Der berechnete Wert von 1, 78 liegt bei 0, 05 auf Signifikanzniveau unter 2, 14.

Daher wird H ₀ akzeptiert. Wir schließen daraus, dass es keinen signifikanten Unterschied zwischen den Durchschnittswerten des Interest Tests von zwei Jungengruppen gibt.

Beispiel 5

In einer Privatschule werden 8 Jungen, deren Verhaltensaufzeichnungen exemplarisch sind, und 5 Jungen, deren Aufzeichnungen sehr schlecht sind, ein Persönlichkeitsinventar verwaltet.

Daten sind unten angegeben:

Ist der Unterschied zwischen Gruppenmitteln auf der 0, 05-Ebene signifikant? auf der 01 Ebene?

Bei der Eingabe von Tabelle D stellen wir fest, dass mit df 11 der kritische Wert von t auf der 0, 05-Ebene 2, 20 und auf der 0, 01-Ebene 3, 11 beträgt. Der berechnete Wert von 2, 28 beträgt nur mehr als 2, 20, aber weniger als 3, 11.

Wir schließen daraus, dass der Unterschied zwischen den Gruppenmittelwerten auf 0, 05-Niveau signifikant ist, auf 0, 01-Pegel jedoch nicht signifikant.

Beispiel 6:

Bei einem arithmetischen Argumentationstest erzielten elf zehnjährige Jungen und sechs zehnjährige Mädchen die folgenden Ergebnisse:

Ist der mittlere Unterschied von 2, 50 auf 0, 05 signifikant?

Lösung:

Durch Anwendung der Formel (43 b).

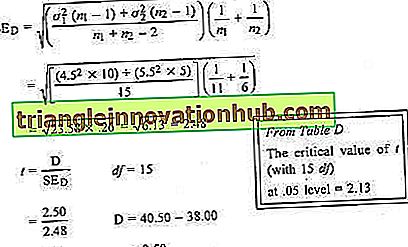
Bei der Eingabe von Tabelle D stellen wir fest, dass mit df 15 der kritische Wert von t auf dem Niveau von 0, 05 2, 13 ist. Der erhaltene Wert von 1, 01 beträgt weniger als 2, 13. Daher ist der deutliche Unterschied von 2, 50 auf dem Niveau von 0, 05 nicht signifikant.

(b) SE der Differenz zwischen zwei korrelierten Mitteln:

(i) Die Einzelgruppenmethode:

Wir haben uns bereits mit dem Problem befasst, zu bestimmen, ob der Unterschied zwischen zwei unabhängigen Mitteln signifikant ist.

Jetzt befassen wir uns mit der Bedeutung des Unterschieds zwischen korrelierten Mitteln. Korrelierte Mittel werden aus demselben Test erhalten, der derselben Gruppe zweimal verabreicht wurde.

Nehmen wir an, wir haben einer Gruppe von Kindern einen Test unterzogen, und nach zwei Wochen müssen wir den Test wiederholen. Wir möchten die Auswirkung von Übung oder Spezialtraining auf die zweite Reihe von Ergebnissen messen. Zur Bestimmung der Signifikanz der Differenz zwischen den bei der Anfangs- und Endprüfung erhaltenen Mittelwerten.

Wir müssen die Formel verwenden:

wobei σ _M1 und σ _M2 = SE's der Anfangs- und Endtesteinrichtung sind

r ₁₂ = Korrelationskoeffizient zwischen den Ergebnissen des ersten und des letzten Tests.

Beispiel 7:

Zu Beginn des akademischen Jahres betrug die durchschnittliche Punktzahl von 81 Schülern nach einem Bildungsleistungstest im Lesen 35 bei einem SD von 5.

Am Ende der Sitzung betrug der Mittelwert für eine äquivalente Form desselben Tests 38 mit einem SD von 4. Die Korrelation zwischen den Ergebnissen des anfänglichen und des abschließenden Tests betrug 0, 53. Hat die Klasse im Laufe des Jahres bedeutende Fortschritte beim Lesen gemacht?

Wir können unsere Daten wie folgt tabellieren:

(Test auf .01 Signifikanzniveau)

Lösung:

Da es uns nur um Fortschritt oder Gewinn geht, ist dies ein einseitiger Test.

Durch Anwenden der Formel:

Da es 81 Schüler gibt, gibt es 81 Paare von Punkten und 81 Unterschiede, so dass der df 81 - 1 oder 80 wird. Aus Tabelle D ist das t für 80 df auf dem Wert von 0, 02 2, 38. (Die Tabelle zeigt 2, 38 für den zweiseitigen Test, 0, 01 für den einseitigen Test.)

Der erhaltene t von 6, 12 ist weit größer als 2, 38. Daher ist der Unterschied signifikant. Es ist sicher, dass die Klasse im Laufe des Schuljahres erhebliche Fortschritte beim Lesen gemacht hat.

(ii) Differenzmethode:

Wenn Gruppen klein sind, verwenden wir die "Differenzmethode" für einfache und schnelle Berechnungen.

Beispiel 8:

Zehn Probanden erhalten fünf aufeinanderfolgende Versuche nach einem Ziffernsymboltest, von denen nur die Ergebnisse für die Versuche 1 und 5 gezeigt werden. Ist der mittlere Gewinn von der ersten bis zur abschließenden Studie signifikant?

Die Differenzsäule wird aus der Differenz zwischen Punktepaaren ermittelt. Die mittlere Differenz beträgt 4 und der SD um diesen Mittelwert (SD _D ).

Berechnung der SE der mittleren Differenz:

In welcher SE _MD = Standardfehler der mittleren Differenz

SD = Standardabweichung um die mittlere Differenz.

Die erhaltene t von 5, 26> 2, 82. Unser t von 5, 26 ist viel größer als das 0, 01-Niveau von 2, 82, und es besteht wenig Zweifel daran, dass der Gewinn von Versuch 1 zu Versuch 5 signifikant ist.

(iii) Die Methode äquivalenter Gruppen:

Paarung:

Manchmal müssen wir die mittlere Leistung von zwei äquivalenten Gruppen vergleichen, die paarweise übereinstimmen.

Bei der Methode der äquivalenten Gruppen wird der Abgleich anfangs paarweise durchgeführt, so dass jede Person in der ersten Gruppe einen Abgleich in der zweiten Gruppe hat.

In diesen Fällen ist die Anzahl der Personen in beiden Gruppen gleich, dh n ₁ = n ₂ .

Hier können wir SE _D mit der Formel berechnen:

wobei SE _{M1 und} SE _M2 = Standardfehler der Endwerte von Gruppe I und Gruppe II sind.

r ₁₂ = Korrelationskoeffizient zwischen den Endwerten der Gruppe I und der Gruppe II.

Beispiel 9:

Basierend auf den Bewertungen, die die Schüler in einem Intelligenztest erhalten hatten, wurden zwei Gruppen gebildet. Eine der Gruppen (Versuchsgruppe) erhielt für einen Monat eine zusätzliche Anweisung und die andere Gruppe (kontrollierte Gruppe) erhielt keine solche Anweisung.

Nach einem Monat erhielten beide Gruppen den gleichen Test, und die Daten zu den endgültigen Ergebnissen sind unten angegeben:

Deutung:

Bei Eingabe der Tabelle von t (Tabelle D) mit df 71 beträgt der kritische Wert von t auf der 0, 05-Ebene im Fall eines einseitigen Tests 1, 67. Die erhaltene t von 2, 34> 1, 67. Daher ist der Unterschied auf dem Niveau von 0, 05 signifikant.

. ^. . Der Mittelwert ist aufgrund zusätzlicher Anweisungen gestiegen.

Mit df von 71 beträgt der kritische Wert von t auf dem 0, 01-Niveau im Fall eines einseitigen Tests 2, 38. So wurde t von 2, 34 <2, 38 erhalten. Daher ist der Unterschied auf dem Niveau von 0, 01 nicht signifikant.

Standardfehler der Differenz zwischen anderen Statistiken:

(i) SE der Differenz zwischen nicht korrigierten Medianen:

Die Signifikanz des Unterschieds zwischen zwei Medianen, die aus unabhängigen Proben erhalten wurden, kann der folgenden Formel entnommen werden:

(ii) SE der Differenz zwischen Standardabweichungen: