Entwerfen von Brücken: Top 14-Checkliste
Die folgenden Lasten, Kräfte und Spannungen sind bei der Konstruktion von Brücken zu berücksichtigen und zu prüfen: - 1. Eigenlast 2. Live-Last 3. Fußbelastung 4. Aufprallschutz 5. Windlast 6. Horizontalkraft aufgrund von Wasserströmungen 7. Längskräfte 8. Zentrifugalkräfte 9. Auftrieb 10. Erddruck 11. Temperatureinflüsse 12. Verformungseffekte 13. Sekundäre Effekte 14. Wellendruck und wenige andere.
Eigengewicht:
Die Einheitsgewichte verschiedener Materialien sind in der Konstruktion wie in Tabelle 5.1 dargestellt anzunehmen.

Alle neuen Straßenbrücken in Indien werden gemäß den Beladungen des Indian Roads Congress entworfen, die aus drei Ladungsklassen bestehen, nämlich der Klasse AA der IRC-Klasse, der Klasse A der Klasse IRC und der Klasse B der Klasse IRC. Für Brücken, die in bestimmten städtischen Grenzen, in Industriegebieten und auf bestimmten festgelegten Autobahnen gebaut werden sollen, sind Einbahnstraßen der Klasse AA oder zwei Fahrstreifen der Klasse A zu berücksichtigen, wobei der jeweils schlechtere Effekt zu berücksichtigen ist.
Alle anderen Festbrücken müssen mit zwei Fahrstreifen der Klasse A beladen werden, während zwei Fahrstreifen der Klasse B auf Brücken in bestimmten Bereichen oder auf temporäre Bauwerke wie Holzbrücken usw. anwendbar sind. Wenn die Klasse 70-R angegeben ist, ist dies der Fall muss anstelle der IRC-Klasse AA verwendet werden. Abb. 5.1 und 5.2 zeigen die IRC-Ladungen.
Es wird davon ausgegangen, dass diese Lasten entlang der Längsachse der Brücken verlaufen und sich an einer beliebigen Stelle des Decks befinden können, um den in dem Abschnitt hervorgerufenen ungünstigsten Effekt zu berücksichtigen, sofern die Abstände zwischen dem Rad und dem Straßenrand, die Abstände zwischen Achsen oder Rädern und Der Abstand zwischen den benachbarten Fahrzeugen, wie im Ladediagramm gezeigt, wird nicht beeinträchtigt.


Alle Achsen eines Standardfahrzeugs oder -zugs gelten als gleichzeitig wirkend, und es wird nicht davon ausgegangen, dass der von dem Standardzug freigelegte Platz keiner zusätzlichen Belastung ausgesetzt ist. Die an der Antriebseinheit angebrachten Anhänger sind nicht als abnehmbar anzusehen.
Alle neuen Brücken müssen entweder einspurig, zweispurig oder vierspurig sein. Dreispurige Brücken werden nicht berücksichtigt. Bei vierspurigen Brücken oder mehreren zweispurigen Brücken ist ein mindestens 1, 2 m breiter Mittellauf vorzusehen.
Verringerung der Belastung durch LL gleichzeitig auf mehr als zwei Fahrspuren:
Die Belastungsintensität kann für jede zusätzliche Fahrspur, die über die beiden Fahrspuren hinausgeht, um 10% verringert werden, wobei die maximale Verringerung um 20% und auch unter der Bedingung verringert wird, dass die so verringerten Belastungsintensitäten nicht unter den resultierenden Intensitäten liegen von einer gleichzeitigen Beladung auf zwei Spuren.
Methode der Anwendung von Live Load für die Gestaltung von Deckplatten:
1. Nur für Platten, die sich in eine Richtung erstrecken:
A. Verteilung der Last senkrecht zur Spannweite:
(a) Massivplatte, die sich in eine Richtung erstreckt:
(i) Für eine einzelne konzentrierte Ladung wird die effektive Breite gemäß der nachstehenden Formel berechnet. Die effektive Breite darf jedoch die tatsächliche Breite der Platte nicht überschreiten.

Wobei b e = die effektive Breite der Bramme, auf die die Last wirkt.
L = die effektive Spanne bei einfach unterstützter Spanne und die freie Spanne bei kontinuierlicher Spanne.
X = Abstand des Schwerpunkts der konzentrierten Last von der näheren Abstützung.
W = die Abmessung der Reifenkontaktfläche in einer Richtung rechtwinklig zur Spannweite plus der doppelten Dicke des Verschleißes der Verschleißschicht.
K = ein Koeffizient mit den in Tabelle 5.2 gezeigten Werten in Abhängigkeit von dem Verhältnis von b / L, wobei b die Breite der Platte ist.

ii) Für zwei oder mehr konzentrierte Lasten in einer Linie in Spannweitenrichtung ist das Biegemoment pro Meter Breite für jede Last entsprechend ihrer geeigneten effektiven Breite separat zu berechnen.
(iii) Wenn bei zwei oder mehr Lasten über die Spannweite die effektive Breite der Bramme für eine Last die effektive Brammenbreite für eine benachbarte Last überschneidet, ist die sich ergebende effektive Breite der Bramme für die beiden Lasten gleich der Summe der jeweiligen effektiven Breite für jede Last minus der Überlappungsbreite, vorausgesetzt, dass die Platte für die zwei getrennt wirkenden Lasten geprüft wird.
(b) Festplattenbrückenträger:
(i) Bei einer einzelnen konzentrierten Last muss die effektive Breite der Platte, die dem Biegemoment (parallel zur unterstützten Kante gemessen) standhält, wie folgt sein:
be = 1, 2x + W (5, 2)
Wobei e, x und W die gleiche Bedeutung wie zuvor haben.
Vorausgesetzt, dass die effektive Breite ein Drittel der parallel zur Auflage gemessenen Länge der Auslegerplatte nicht überschreiten darf und auch, wenn die effektive Breite die Hälfte des obigen Werts zuzüglich des Abstandes der konzentrierten Last vom näheren äußersten Ende nicht überschreitet konzentrierte Last wird in der Nähe eines der beiden äußersten Enden der Auslegerplatte angeordnet.
ii) Für zwei oder mehr konzentrierte Ladungen:
Wenn die effektive Breite der Platte für eine Last die effektive Breite für eine benachbarte Last überlappt, ist die resultierende effektive Breite für zwei Lasten gleich der Summe der jeweiligen effektiven Breiten für jede Last abzüglich der Breite der Überlappung, sofern die Platte vorhanden ist So ausgelegt ist für die beiden getrennt wirkenden Lasten getestet.
B. Verteilung der Last entlang der Spanne:
Die effektive Länge der Bramme, auf die eine Radlast oder eine Riegellast wirkt, ist gleich den Abmessungen der Reifenkontaktfläche über der Verschleißfläche der Bramme in Richtung der Spanne zuzüglich der doppelten Gesamttiefe der Bramme einschließlich die Dicke des tragenden Mantels.
2. Für Platten, die sich in zwei Richtungen erstrecken, und für Platten, die sich in eine Richtung erstrecken und eine Breite haben, die das 3-fache der effektiven Spannweite übersteigt:
Nehmen Sie ein Einflussfeld, Piegeauds oder eine andere rationale Methode mit einem Wert von Poisson von 0, 15 an.
3. Für gerippte Platten oder andere Platten als Vollplatten:
Wenn das Verhältnis der Biegesteifigkeit in Querrichtung zur Biegesteifigkeit in Längsrichtung Eins beträgt, können die effektiven Breiten wie für die Massivplatte berechnet werden. Wenn das Verhältnis kleiner als Eins ist, wird ein proportional kleinerer Wert verwendet.
4. Verteilung der Lasten durch Füllungen und Deckschicht:
Die Verteilung der Lasten durch Füllungen und Verschleißschichten ist bei 45 Grad entlang und senkrecht zur Spannweite vorzunehmen.
Fußweg laden:
Bei einer effektiven Spannweite von 7, 5 m oder weniger: 400 kg / m 2 . Diese Belastung wird für Brücken in der Nähe einer Wallfahrtsstadt oder eines großen Kirchentreffs auf 500 kg / m 2 erhöht.
Bei einer effektiven Spannweite von mehr als 7, 5 m bis 30 m darf die Belastungsintensität nach folgender Gleichung berechnet werden:

Für effektive Spannweiten von mehr als 30 m ist die Intensität der Fußbelastung nach folgender Formel zu bestimmen:

Wenn P '= 400 kg / m 2 ist, kann dies der Fall sein
P = Fußbelastung in kg pro m 2
L = effektive Spannweite des Hauptträgers in Metern
W = Fußweg in Metern
Die Trittfläche muss so ausgelegt sein, dass sie einer Belastung von 4 Tonnen einschließlich eines Aufpralls, der über einen Bereich mit einem Durchmesser von 300 mm verteilt ist, standhält. In diesem Fall können die zulässigen Spannungen um 25 Prozent erhöht werden, um diese Bestimmung zu erfüllen. Wenn die Fahrzeuge den Fußweg nicht befahren können, muss diese Bestimmung nicht getroffen werden.
Aufwandsentschädigung:
Die Aufwandsentschädigung als Prozentsatz der angewendeten aktiven Lasten ist für die dynamische Wirkung der aktiven Lasten wie folgt zu berücksichtigen:
Für Klasse A oder Klasse B Laden:
Der Prozentsatz der Auswirkungen muss dem in Abbildung 5.3 entsprechen. Der Schlaganteil wird nach folgenden Formeln für die Spannweiten von 3 m bis 45 m berechnet:

a) Für Stahlbetonbrücken:
Schlagfraktion = 4, 5 / 6 + L
b) Für Stahlbrücken:
Schlagfraktion = 9 / 13, 5 + L
Wobei L = Länge der Spannweite in Metern wie angegeben
Für das Laden der Klasse AA und das Laden der Klasse 70R:
Der Prozentsatz der Auswirkungen ist wie folgt zu verstehen:
A. Für eine Spannweite von weniger als 9 m:
i) Bei Kettenfahrzeugen - 25% bei Spannweiten von bis zu 5 m, linear zu 10% bei Spannweiten von 9 m.
ii) bei Radfahrzeugen - 25%.
B. Für Spannweiten von 9 m oder mehr:
(a) Stahlbetonbrücken:
(i) Raupenfahrzeuge: 10% bis zu einer Spannweite von 40 m und entsprechend der Kurve in Abb. 5.3 für Spannweiten von mehr als 40 m.
(ii) Fahrzeuge mit Rädern: 25% bei Spannweiten bis 12 m und gemäß der Kurve in Abb. 5.3 bei Spannweiten über 12 m.
(b) Stahlbrücken :
(i) Raupenfahrzeuge: 10% für alle Strecken.
(ii) Fahrzeuge mit Rädern: 25% für Spannweiten bis 23 m und gemäß der in Abb. 5.3 angegebenen Kurve für Spannweiten über 23 m.
Auf die Trittbelastung darf kein Aufprall zugelassen werden. Bei Brückenkonstruktionen mit einer Füllung von mindestens 600 mm einschließlich der Straßenkruste muss der Prozentsatz der Auswirkungen bei der Hälfte der in der Klasse A oder Klasse B angegebenen und der Klasse AA und der Klasse 70R liegen.
Für die Berechnung der Spannungen an verschiedenen Punkten von Pfeilern und Widerlagern von oben auf dem Bettblock sind die Prozentsätze der Auswirkungen in den folgenden Anteilen zulässig:
(i) Druck auf die Lager und die Oberfläche des Bettblocks Voller Wert
(ii) Unterseite des Bettblockhalbwerts
(iii) Von der Bodenfläche des Bettblocks bis zu 3 m der Struktur unter dem Bettblock halbieren und gleichmßig auf Null abnehmen
(iv) 3 m unter dem Boden des Bettblocks Null
Die Spannweite L, die bei der Berechnung der Aufprallprozentsätze berücksichtigt werden muss, wie in Klasse A oder Klasse B angegeben, Ladung und Klasse AA, und Klasse 70R, ist wie folgt:
(a) Für einfach abgestützte oder durchgehende Spannweiten oder für Bögen ist L = die effektive Spannweite, auf die die Last aufgebracht wird.
(b) Bei Brücken mit Auslegerarmen ohne Schwebeflanken ist L = der effektive Überhang des Auslegers um 25% für die Belastung des Auslegerarms und L = die effektive Spanne zwischen den Stützen für die Hauptspannung.
(c) Bei Brücken mit Auslegerarmen mit aufgehängten Spannweiten ist L = der effektive Überhang des Auslegerarms zuzüglich der halben Länge der aufgehängten Spannweite für die Belastung des Auslegerarms und L = der effektiven Länge der aufgehängten Spannweite für die aufgehängten Lasten Spannweite und 'L = die effektive Spannweite zwischen den Stützen für die Belastung der Hauptspanne.
Windlast:
Es wird angenommen, dass die Windlast auf jeden freiliegenden Teil der Brückenkonstruktion horizontal wirkt. Die Richtung der Windlast kann so sein, dass maximale resultierende Spannungen in dem betrachteten Element erzeugt werden.
Es wird angenommen, dass die Windstärke auf den Bereich der Struktur wie folgt wirkt:
(a) Bei Deckskonstruktionen - der in der Ansicht gesehene Bereich der Konstruktion einschließlich des Bodensystems und des Geländers ohne die Perforationsfläche in den Handläufen oder Brüstungswänden.
(b) Für eine durchgehende oder eine halbe durchgehende Konstruktion - der unter (a) oben angegebene Bereich der Erhebung des Luv-Fachwerkteils plus die Hälfte des Erhöhungsbereichs oberhalb der Deckhöhe aller anderen Traversen oder Träger.
Die Intensität des Winddrucks muss der nachstehenden Tabelle 5.3 entsprechen. In bestimmten Küstengebieten wie der Halbinsel Kathiawar, Bengalen und Orissa kann die Intensität verdoppelt werden, wie in der Karte dargestellt (Abb. 5.4).


Woher
H = Die durchschnittliche Höhe der exponierten Fläche in Metern über der mittleren Verzögerungsfläche (Boden, Bett oder Wasserstand).
V = Windgeschwindigkeit in km pro Stunde.
P = Intensität des Winddrucks in Kg / m 2 in der Höhe H
Es wird angenommen, dass die Windlast für die bewegte Nutzlast bei gewöhnlichen Brücken 1, 5 m über der Fahrbahn mit 300 kg pro laufendem Meter Nutzlast und 450 kg pro Meter bei Brücken mit Straßenbahn wirkt.
Die Gesamtwindstärke darf nicht weniger als 450 kg pro Laufmeter in der Ebene des belasteten Gurtes und 225 Kg pro Laufmeter im unbelasteten Gurt auf durchgehender oder halb durchgeführter Traverse, Gitter oder ähnlichen Feldern und nicht weniger als 450 betragen Kg pro Laufmeter auf Deckspannweiten.
Ein Winddruck von 240 kg pro Meter auf die unbelastete Konstruktion muss auch berücksichtigt werden, wenn er größere Spannungen als die zuvor genannten Windlasten erzeugt.
Horizontale Kraft aufgrund von Wasserströmungen:
Die Auswirkung der Horizontalkraft aufgrund von Wasserströmungen muss bei der Gestaltung eines Teils der Brückenkonstruktion berücksichtigt werden, der in fließendes Wasser eingetaucht ist.
Die Intensität des Wasserdrucks aufgrund der Wasserströmung kann nach folgender Formel berechnet werden:
Woher:
P = Druckintensität in Kg / m2
U = die Geschwindigkeit der Wasserströmung am betrachteten Punkt in Meter pro Sekunde.
K = Eine Konstante mit den Werten für verschiedene Pfeilerformen (siehe Tabelle 5.4)

Es kann angenommen werden, dass die Variation von U 2 mit dem Nullwert bei maximalem Spülniveau und dem Quadrat der maximalen Geschwindigkeit an der Oberfläche linear ist (Abb. 5.5). Die maximale Oberflächengeschwindigkeit V kann als Vm √2 angenommen werden, dh V2s = 2 V2m wobei Vm die mittlere Geschwindigkeit ist.
Daher ist U 2 in Gleichung 5, 7 in einer Tiefe X von der maximalen Reinigungsstufe gegeben durch:


Um einer möglichen Änderung der Richtung des Wasserstroms von der normalen Flussrichtung entgegenzuwirken, kann bei der Konstruktion eine Vorkehrung getroffen werden, indem eine Neigung des Wasserstroms um 20 Grad gegenüber der normalen Flussrichtung angenommen wird.
Die Geschwindigkeit soll in solchen Fällen in zwei Komponenten zerlegt werden, nämlich eine parallel und die andere normal zum pier. Die Werte von K für die Normalkomponente sind mit 1, 5 anzunehmen, außer für kreisförmige Pfeiler, wenn K als 0, 66 angenommen werden kann.
Längskräfte:
Die Auswirkungen von Längskräften aufgrund von Zugkraft oder Bremswirkung (wobei letztere größer als die erstgenannten sind) und der Reibungswiderstand, den das Freilager aufgrund von Temperaturänderungen oder anderen Ursachen bietet, sind bei der Auslegung des Systems zu berücksichtigen Lager, Unterbauten und Fundamente.
Es wird angenommen, dass die Horizontalkraft durch Zug oder Bremsen entlang der Fahrbahn und in 1, 2 Meter Höhe wirkt.
Die Brems- und Temperatureinflüsse auf Brücken Konstruktionen ohne Lager wie Bögen, starre Rahmen usw. sind gemäß der genehmigten Analysemethode für unbestimmte Konstruktionen zu berücksichtigen.
Bei einfach abgestützten Stahlbeton- und Spannbetonkonstruktionen können Plattenlager nicht für Spannweiten von mehr als 15 Metern verwendet werden.
Bei einfach unterstützten Spannweiten von bis zu 10 Metern, in denen keine Lager (außer Bitumenschicht) vorgesehen sind, muss die Horizontalkraft auf Lagerebene
F / 2 oder µ Rg, je nachdem, welcher Wert höher ist
Wobei F = aufgebrachte Horizontalkraft
µ = Reibungskoeffizient wie in Tabelle 5.5 angegeben
Rg = Reaktion aufgrund einer toten Last.
Die Längskraft an jedem freien Lager (Gleit- oder Rollenlager) für eine einfach gestützte Brücke ist als gleich µR zu verstehen, wobei i der Reibungskoeffizient und R die Summe der Tot- und Lastlastreaktion ist. Die Werte von p. wie in Tabelle 5.5 gezeigt, wird im Design normalerweise angenommen.

Die Längskraft an einem Festlager für eine einfach gelagerte Brücke muss wie folgt sein:
F - µR oder F / 2 + µR, je nachdem, welcher Wert größer ist
Wobei F = aufgebrachte Horizontalkraft
µ = Reibungskoeffizient wie in Tabelle 5.5 angegeben
R = Reaktion wegen Totlast.
Die Längskraft an jedem Ende einer einfach gehaltenen Struktur mit identischen elastomeren Lagern ist gegeben durch F / 2 V δ, wobei V r die Scherfestigkeit des elastomeren Lagers ist und 8 die Bewegung des Bodens aufgrund von Temperatur usw. ist, die nicht der Regel entspricht aufgebrachte Kräfte.
Die Längskräfte auf Stützen einer durchgehenden Struktur werden auf der Grundlage der Scherleistung der einzelnen Stützen und des Nullbewegungspunkts des Decks bestimmt.
Die Längs- und alle anderen Horizontalkräfte sind bis zu dem Niveau zu berechnen, bei dem der resultierende passive Erddruck des Bodens unterhalb des tiefsten Gießniveaus (oder das Bodenniveau bei einer Brücke mit Pucca-Boden) diese Kräfte ausgleicht.
Es wird angenommen, dass die Bremswirkung folgende Werte hat:
(i) Bei einem einspurigen oder zweispurigen Brückendeck beträgt die Bremswirkung für den ersten Zug des Fahrzeugs zwanzig Prozent, für die nachfolgenden Züge oder einen Teil davon zehn Prozent.
Bei der Berechnung der Bremswirkung muss nur eine Spur der Zuglasten berücksichtigt werden, selbst wenn das Brückendeck zwei Spuren der Zuglasten trägt. Die Bremswirkung muss zwanzig Prozent der Last betragen, die sich tatsächlich auf der Spanne befindet, bei der sich der gesamte erste Zug nicht auf der Spanne befindet.
(ii) Bei Brücken mit mehr als zwei Fahrspuren ist die Bremswirkung gleich dem unter (i) für zwei Fahrspuren angegebenen Wert zuzüglich fünf Prozent der auf den Fahrspuren befindlichen Last von mehr als zwei anzunehmen.
Zentrifugalkräfte:
Bei einer gekrümmten Brücke muss die Wirkung der Fliehkraft aufgrund der Bewegung der Fahrzeuge in einer Kurve angemessen berücksichtigt werden, und die Glieder müssen so ausgelegt sein, dass sie den durch die Fliehkraftwirkung hervorgerufenen zusätzlichen Belastungen Rechnung tragen.
Die Fliehkraft ist nach folgender Formel zu berechnen:
C = WV 2 / 127R (5, 8)
Dabei gilt: C = Fliehkraft in Tonnen
W = Gesamtlast in Tonnen über die Spannweite
V = Konstruktionsgeschwindigkeit in km pro Stunde
R = Krümmungsradius in Metern
Es wird angenommen, dass die Fliehkraft in einer Höhe von 1, 2 m über der Fahrbahn wirkt. Eine Erhöhung der Schlagwirkung ist nicht erforderlich. Es wird angenommen, dass die Fliehkraft am Angriffspunkt der Radlasten wirkt oder gleichmäßig über die Länge verteilt ist, auf die eine gleichmäßig verteilte Last wirkt.
Auftrieb:
Die Auswirkung des Auftriebs muss bei der Gestaltung der Brückenkonstruktionen berücksichtigt werden, wenn diese Überlegung die schlechteste Auswirkung auf das Glied hat. Aufgrund des Auftriebs wird das Gewicht der Konstruktion reduziert.
Wenn das Fundament auf homogenen undurchlässigen Schichten ruht, ist keine Vorkehrung für den Auftriebseffekt zu treffen. Wenn das Fundament dagegen auf durchlässigen Schichten wie Sand, Schluff usw. ruht, wird der volle Auftrieb berücksichtigt. Für andere Gründungsbedingungen, einschließlich der Gründung auf Fels, wird nach Ermessen des Brückendesigners ein gewisser Prozentsatz des vollen Auftriebs als Auftriebseffekt angenommen.
Als Auftriebseffekt für untergetauchte Beton- oder Ziegelmauerkonstruktionen aufgrund von Porendruck werden 15% des vollen Auftriebs angenommen.
Die Wirkung des vollen Auftriebs ist bei der Konstruktion der Überstruktur für Unterwasserbrücken gebührend zu berücksichtigen, wenn sie größere Spannungen erzeugt.
Bei tiefen Fundamenten, die sowohl Wasser als auch Bodenmasse wie Sand, Schluff usw. verdrängen, ist der Auftrieb, der die Gewichtsabnahme bewirkt, aus zwei Gründen zu berücksichtigen:
(i) Der Auftrieb aufgrund von verdrängtem Wasser ist als Gewicht des von der Konstruktion verdrängten Wasservolumens von der freien Wasseroberfläche bis zur Fundamentebene zu verstehen.
(ii) Aufwärtsdruck aufgrund des eingetauchten Bodens, berechnet gemäß Rankines Theorie.
Erddruck:
Der Erddruck, für den Erdrückhaltestrukturen ausgelegt werden sollen, muss gemäß jeder rationalen Theorie berechnet werden. Die Coulomb-Erddrucktheorie kann angewendet werden, sofern davon ausgegangen wird, dass der resultierende Erddruck in einer Höhe von 0, 42 H von der Basis aus wirkt, wobei H die Höhe der Stützmauer ist.
Es wird angenommen, dass die Mindestintensität des horizontalen Erddrucks nicht geringer ist als der Druck, der von einer Flüssigkeit mit einem Gewicht von 480 kg pro Cum ausgeübt wird. Alle Aufbauten müssen für einen Auflastzuschlag in Höhe von 1, 2 m Erdschüttung ausgelegt sein. Für die Bemessung der Trag- und Rückwände ist der Auflastzuschlag auf 0, 6 m Höhe der Erdschüttung anzusetzen.
Die Füllungen hinter den Widerlagern, Flügeln und Rückwänden, die den Erddruck ausüben, müssen aus körnigen Materialien bestehen. Auf der gesamten Oberfläche der Abutments, der Flügel oder der Rückwände ist ein Filtermedium mit einer Dicke von 600 mm mit einer kleineren Größe in Richtung Boden und einer größeren Größe in Richtung der Wand vorzusehen.
In den Widerlagern, Flügeln oder Rückwänden oberhalb des niedrigen Wasserspiegels muss eine ausreichende Anzahl von Tränenlöchern vorgesehen sein, um das angesammelte Wasser hinter den Wänden ableiten zu können. Der Abstand der Wischlöcher darf sowohl in horizontaler als auch in vertikaler Richtung einen Meter nicht überschreiten. Die Größe der Austrittsöffnungen muss für eine ordnungsgemäße Entwässerung ausreichen und die Austrittsöffnungen müssen zur Außenseite hin geneigt sein.
Temperatureffekte:
Alle Bauwerke müssen so ausgelegt sein, dass sie den durch Temperaturschwankungen entstehenden Spannungen gerecht werden. Die Variationsbreite muss für den Ort, an dem die Struktur erstellt werden soll, sinnvoll festgelegt werden.
Die Verzögerung zwischen der Lufttemperatur und der Innentemperatur massiver Betonbauteile ist gebührend zu berücksichtigen. Der in Tabelle 5.6 dargestellte Temperaturbereich ist generell bei der Auslegung anzunehmen.

Der Ausdehnungskoeffizient pro Grad Celsius wird für Stahl- und RC-Konstruktionen mit 11, 7 x 10 -6 und für einfache Betonkonstruktionen mit 10, 8 x 10 -6 angenommen .
Deformationseffekte (nur für Stahlbrücken):
Die Verformungsspannung wird durch Verbiegen eines Teils eines Trägers mit offener Bahn aufgrund der vertikalen Durchbiegung des Trägers in Verbindung mit der Steifigkeit der Verbindungen verursacht. Alle Stahlbrücken müssen so konstruiert, gefertigt und aufgestellt werden, dass die Verformungsspannungen auf ein Minimum reduziert werden. Ohne Bemessungsberechnungen dürfen die Verformungsspannungen nicht weniger als 16% der Last- und Lastlastspannungen betragen.
Sekundäre Effekte:
Stahlgerüst:
Sekundärspannungen sind zusätzliche Spannungen, die durch die Exzentrizität von Verbindungen verursacht werden, Bodenkörperlasten, die an Zwischenpunkten in einer Platte ausgeübt werden, seitliche Windlasten an den Endpfosten von durchgehenden Traversen usw. und Spannungen aufgrund der Bewegung von Stützen.
Stahlbetonkonstruktionen:
Sekundärspannungen sind zusätzliche Spannungen, die durch die Bewegung von Stützen oder durch die Verformung der geometrischen Form der Struktur oder das einschränkende Schrumpfen von Betonbodenträgern usw. verursacht werden. Bei Stahlbetonkonstruktionen sind die Schwindungskoeffizienten mit 2 x 10 -4 anzusetzen . Alle Brücken sind so auszulegen und zu bauen, dass die Sekundärspannungen auf ein Minimum reduziert werden.
Wellendruck:
Die Wellenkräfte sind durch geeignete Analyse unter Berücksichtigung von Zug- und Trägheitskräften usw. an einzelnen Strukturelementen auf der Grundlage rationaler Methoden oder Modellstudien zu bestimmen. Bei einer Gruppe von Pfeilern, Pfeilern usw. sind auch Annäherungseffekte zu berücksichtigen.
Auswirkungen durch schwimmende Körper oder Schiffe:
Mitglieder wie Brückenpfeiler, Pfahlböcke usw., die Aufprallkräften von Schwimmkörpern oder Schiffen ausgesetzt sind, müssen unter Berücksichtigung der Auswirkungen des Aufpralls auf diese Mitglieder ausgelegt werden. Wenn die Aufprallkraft in einem Winkel auf die Glieder auftrifft, muss auch die Wirkung der Teilkräfte berücksichtigt werden.
Erektionseffekte:
Dem Konstruktionsbüro sind das Montageprogramm und die Reihenfolge der Konstruktionen, die der Konstrukteur übernehmen möchte, zur Verfügung zu stellen, und der Konstrukteur muss die durch die Montageeffekte verursachten Beanspruchungen berücksichtigen. Dazu gehört, dass ein Feld komplett ist und das angrenzende Feld nicht in Position ist.
Seismische Kraft:
Abb. 5.6 zeigt die Karte von Indien, in der die seismische Zone I bis Zone V angegeben ist. Alle Brücken in Zone V müssen für die unten angegebenen seismischen Kräfte ausgelegt sein. Alle größeren Brücken mit einer Gesamtlänge von mehr als 60 Metern müssen auch für die Erdbebeneinwirkung in Zone III und IV ausgelegt sein. Brücken in Zone I und II müssen nicht für seismische Kräfte ausgelegt werden.
Die vertikale seismische Kraft ist bei der Bemessung von Brücken zu berücksichtigen, die in Zone IV und V zu errichten sind und bei denen die Stabilität ein Konstruktionskriterium ist. Der vertikale seismische Koeffizient wird als die Hälfte des horizontalen seismischen Koeffizienten wie nachstehend angegeben angenommen.
Wenn der seismische Effekt in Betracht gezogen wird, muss die Suche nach der Gestaltung des Fundaments auf der mittleren Entwurfsflut basieren. Wenn keine Detaildaten vorliegen, kann die Reinigung mit dem 0, 9-fachen der maximalen Tiefe der Reinigung angenommen werden.
Horizontale seismische Kraft:
Die horizontale seismische Kraft wird durch den folgenden Ausdruck bestimmt, der für Brücken mit einer Spannweite von bis zu 150 m gilt. Bei Brücken mit großer Spannweite und Spannweiten von mehr als 150 m muss der Entwurf auf einem dynamischen Ansatz basieren.
F eq = α. Β. Ƴ. G
Wobei F eq = Seismische Kraft
α = Horizontaler seismischer Koeffizient in Abhängigkeit von der in Tabelle 5.7 angegebenen Position (für Abschnitte unterhalb der Durchdringungstiefe kann dies als Null angenommen werden).
β = Ein Koeffizient in Abhängigkeit vom Bodenfundamentsystem gemäß Tabelle 5.8.
α = Ein Koeffizient in Abhängigkeit von der Bedeutung der Brücke, wie unten angegeben. Die Wichtigkeit wird unter Berücksichtigung lokaler Bedingungen wie strategischer Bedeutung, wichtiger Kommunikationsverbindung usw. festgelegt.
(a) Wichtige Brücke 1.5
(b) Andere Brücken 1.0
G = Leerlast oder Tot plus Stromlast
Die horizontalen seismischen Kräfte müssen im Schwerpunkt aller betrachteten Lasten wirken. Die Richtung der seismischen Kraft muss so sein, dass die resultierende Wirkung der seismischen Kraft und anderer Kräfte maximale Spannungen in der Struktur erzeugt.

Die seismische Kraft für stromführende Lasten darf nicht berücksichtigt werden, wenn sie in Verkehrsrichtung wirkt, sondern in senkrechter Richtung zum Verkehr.

Der in den Boden eingebettete Teil des Bauwerks darf keine seismischen Kräfte erzeugen. In lockeren oder schlecht abgestuften Sanden mit geringen oder keinen Feinteilen können die Vibrationen aufgrund der Erdbebeneinwirkung eine Verflüssigung des Bodens oder eine übermäßige Gesamt- und Differenzbildung verursachen. Daher ist die Errichtung von Brücken auf solchen Schichten in den Zonen III, IV und V zu vermeiden, sofern nicht geeignete Verdichtungs- oder Stabilisierungsmethoden angewandt werden.
Mauerwerke oder Stahlbetonbrücken dürfen nicht in Zone V errichtet werden.

Liniendiagramme beeinflussen:
Alle Bauteile müssen mit Belastungen, Kräften und Belastungen ausgelegt sein, die zusammenwirken können. Die meisten dieser Lasten und Kräfte haben einen mehr oder weniger festen Angriffspunkt, mit Ausnahme der aktiven Lasten und der Kräfte, die von aktiven Lasten herrühren, wie zum Beispiel Aufprallkraft, Zug- oder Bremskraft und Fliehkraft.
Da Live-Lasten bewegte Lasten sind, müssen ihre Angriffspunkte sorgfältig bestimmt werden, um eine maximale Wirkung zu erzielen. Dies wird mit Hilfe von Einflussliniendiagrammen erreicht, wie in den folgenden Abschnitten beschrieben.
Eine Einflusslinie ist eine Kurve, die die Reaktion, das Moment, die Scherung, den Schub usw. eines Abschnitts eines Balkens oder anderer Elemente aufgrund der Bewegung einer konzentrierten Lasteinheit entlang der Länge des Balkens oder Elements angibt.
Das Verfahren zum Zeichnen eines Einflussliniendiagramms wird in den folgenden Abschnitten veranschaulicht. Beeinflussung der Liniendiagramme für einige spezielle Strukturen wie RC-Brücken und RC-Bogenbrücken. Verwendung dieser Einflussliniendiagramme zur Bestimmung von Maximalwerten von Momenten, Scheren, Reaktionen usw.
Liniendiagramm für Moment beeinflussen:
Einfach unterstützter Bridge-Abschnitt bei 0.25L und 0.5L:
Wenn in 5.7 (a) eine Einheitslast zwischen A und X platziert wird (dh der betrachtete Abschnitt), gilt R B = a / L und M x = (ax 0, 75 L) / L, aber wenn die Einheitslast zwischen liegt X und B, RA = (La) / L und Mx = (La) 0, 25L / L. Der Wert von M x ist maximal, wenn die Einheitslast bei X liegt, dh der betrachtete Abschnitt und der Wert von M x = 0, 1875L. Das Einflussliniendiagramm für M x bei 0.25L ist in Abb. 5.7 (c) dargestellt.

Auf ähnliche Weise ist in Fig. 5.7 (b), wenn die Einheitslast zwischen A und X angeordnet ist, M x = ax 0, 5L / L, aber wenn die Einheitslast zwischen X und B angeordnet ist, ist M x = (La) x 0, 5 L / L Der Wert von M x Maximum, wenn die Ladeeinheit auf X gesetzt wird. In diesem Fall ist M x = 0, 25 L. Das Einflussliniendiagramm für M bei 0.5L ist in Abb. 5.7 (d) dargestellt.
Balanced Cantilever Bridge - Abschnitt in der Mitte der Hauptspanne und im Bereich der Unterstützung:
Die Diagramme der Einflusslinien können auf die gleiche Weise gezeichnet werden, wie in Abb. 5.8 dargestellt.

Einflussliniendiagramm für die Scherung:
Einfach unterstützte Bridge - Section bei 0.25L und 0.5L:
Bezugnehmend auf Fig. 5.7 (a), wenn die Einheitslast zwischen A und X (dh dem betrachteten Abschnitt) angeordnet ist, ist R B = a / LS x (dh Scherung bei X) = R B = a / L. Nach der üblichen Konvention ist diese Schubkraft, dh resultierende Kräfte, die auf der rechten Seite des Abschnitts nach oben und auf der linken Seite des Abschnitts nach unten wirken, negativ.
Wenn die Einheitslast zwischen X und B liegt, ist RA = (La / L) und S x (Scherung bei x) = (La / L). Diese Scherung ist wie üblich positiv. Die Scherung ändert das Vorzeichen, wenn die Einheitslast bei X liegt. Daher ist das Einflussliniendiagramm für die Scherung in Abschnitt 0.25L wie in Abb. 5.9 (a) dargestellt. Die Ordinate der negativen Scherung bei X = 0, 25L / L = 0, 25 und die Ordinate der positiven Scherung = L - 0, 25L / L = 0, 75
Bezug nehmend auf Fig. 5.7 (b) kann wie zuvor festgestellt werden, dass, wenn die Einheitslast zwischen A und X liegt, S x = a / L ist und wenn die Einheitslast zwischen X und B liegt, S, = (La / L) . Das Scherungsvorzeichen ändert sich, wenn die Einheitslast bei dem Abschnitt liegt, dh bei 0, 5 l und die Ordinaten sowohl für positive als auch für negative Scherung 0, 5 sind. Das Einflussliniendiagramm ist in Abb. 5.9 (b) dargestellt.

Balanced Cantilever Bridge - Abschnitt in der Mitte der Hauptspanne und im Bereich der Unterstützung:
i) Schnitt in der Mitte der Hauptspanne:
Bezugnehmend auf Fig. 5.8 (a) ist die Reaktion bei D, wenn sich die Einheitslast von A nach G bewegt (dh der betrachtete Abschnitt), wie folgt:

Wenn sich jedoch die Ladeeinheit von G nach F bewegt, Die Reaktion bei C ist wie folgt:

Die Reaktionen R c oder R D sind die Scherung in Abschnitt G. Unter Verwendung der normalen Vorzeichenkonvention ist das Einflussliniendiagramm für die Scherung in Abschnitt G wie in Abb. 5.10 (a) gezeigt.
ii) Abschnitt links von Support C:
Bezug nehmend auf Fig. 5.8 (a) ist die Scherung links von der Unterstützung C die Last bei C, wenn sich die Einheitslast von A nach C und von Null über C hinaus bewegt. Daher ist das Scherkraftliniendiagramm wie in Fig. 5.10 gezeigt (b).
iii) Abschnitt zu Recht auf Unterstützung C:
Bezugnehmend auf Fig. 5.8 (a) ist, wenn sich die Einheitslast von A nach C bewegt, die Scherung numerisch gleich Rd und wenn sich die Einheitslast über C hinaus bewegt, ist die Scherung numerisch gleich Rc. Das Scherkraftliniendiagramm ist in Abb. 5.10 (c) dargestellt.
Zulässige Spannungen:
Konkrete Mitglieder:
Die zulässigen Spannungen für Beton verschiedener Güteklassen sind in Tabelle 5.9 angegeben:

Hinweis:
Für die Berechnung der Spannungen im Schnitt kann ein modulares Verhältnis (E s / E c ) von 10 verwendet werden

Die zulässigen Spannungen in der Stahlbewehrung müssen den Angaben in Tabelle 5.10 entsprechen

Die zulässigen Zugspannungen im Normalbeton sind in Tabelle 5.11 angegeben:

Stahlbetonbauteile können ohne Schubbewehrung ausgeführt werden, wenn die Schubspannung x <Xc gilt, wobei Xc durch folgenden Ausdruck gegeben ist:


Die Bemessungsschubspannung τ = V / bd darf niemals die maximal zulässige Scherung τ max überschreiten, wie nachstehend angegeben:
τ max = 0, 07 f ck oder 2, 5 MP a, je nachdem, welcher Wert niedriger ist. Wobei f ck die charakteristische Festigkeit von Beton ist.
Vorgespannte Betonelemente:
Qualität des Betons:
Die charakteristische Druckfestigkeit von Beton darf nicht weniger als 35 MP betragen, d. H. Die Sorte M 35, mit Ausnahme der Verbundbauweise, bei der Beton der Sorte M 30 für Deckplatten zugelassen werden könnte.
Zulässige temporäre Spannungen in Beton:
Diese Spannungen werden nach Berücksichtigung aller Verluste berechnet, außer durch Restschwindung und Kriechen des Betons. Die zeitweilige Druckspannung darf 0, 5 f Cj nicht überschreiten, die nicht mehr als 20 MPa betragen darf, wobei f Cj die Betonfestigkeit zu diesem Zeitpunkt ist, für die ein Höchstwert von f ck gilt .
Bei voller Übertragung darf die Würfelfestigkeit von Beton nicht weniger als 0, 8 f tk betragen . Die vorübergehende Druckspannung in den extremen Betonfasern (einschließlich der Vorspannung der Stufen) darf 0, 45 f ck ( max. 20 MPa) nicht übersteigen.
Die vorübergehende Zugspannung in der extremen Faser darf nicht übersteigen 1/10 der zulässigen temporären Druckspannung im Beton.
Zulässige Betonspannungen während des Betriebs:
Die Druckspannung im Beton während des Betriebs darf 0, 33 f ck nicht überschreiten. Während des Betriebs ist im Beton keine Zugspannung zulässig.
Wenn vorgefertigte Segmentelemente durch Vorspannung zusammengefügt werden, müssen die Spannungen in der extremen Betonfaser während des Betriebs immer druckbeaufschlagt sein und die minimale Druckspannung in einer extremen Faser muss mindestens 5% der maximalen dauerhaften Druckspannung betragen kann in demselben Abschnitt entwickelt werden. Diese Bestimmung gilt jedoch nicht für quer vorgespannte Deckplatten.
Zulässige Lagerspannung hinter Verankerungen:
Die maximal zulässige Spannung unmittelbar hinter den Verankerungen in ausreichend verstärkten Endblöcken kann durch folgende Gleichung berechnet werden:
f b = 0, 48 f cj √A 2 / A 1 0r 0, 8 f cj, je nachdem, welcher Wert kleiner ist
Dabei ist f b = die zulässige Druckkontaktspannung in Beton einschließlich der auftretenden Spannungen wie bei Zwischenverankerungen.
A 1 = die tragende Fläche der Verankerung, deren Form in ein Quadrat gleichwertiger Fläche umgewandelt wird
A 2 = maximale Fläche des Quadrats, die innerhalb des Elements enthalten sein kann, ohne die entsprechende Fläche benachbarter Verankerungen zu überdecken und konzentrisch mit der Lagerfläche A 1.
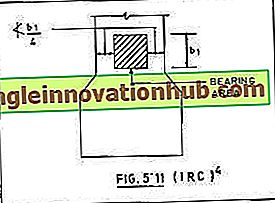
Der oben genannte Wert der Lagerbelastung ist nur zulässig, wenn ein Betonüberstand von mindestens 50 mm oder b 1/4 vorhanden ist, je nachdem, welcher Bereich der Verankerung stärker ist, wobei bi wie in Abb. 5.11 dargestellt ist.
Zulässige Spannungen im Vorspannungsstahl:
Die maximale temporäre Spannung in dem Spannstahl an einem beliebigen Abschnitt nach Berücksichtigung von Verlusten durch Verankerung und elastisches Verkürzen darf 70% der Mindestzugfestigkeit nicht überschreiten.
Eine Überbeanspruchung zum Ausgleich des Verrutschens von Verankerungen oder zur Erzielung einer kalkulierten Dehnung kann zulässig sein, wenn die Anpresskraft auf 80% der Mindestzugfestigkeit oder 95% der Dehngrenze (0, 2%) des Spannstahls begrenzt ist was auch immer weniger ist.